
 某市为增强市民的环境保护意识,某市组织了一批年龄在[20,45]岁的志愿者为市民展开宣传活动,现从这批志愿者中随机抽取100名按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45],各组人数的频率分布直方图如图所示,现从第3,4,5组中用分层抽样的方法抽取6名志愿者参加宣传活动.
某市为增强市民的环境保护意识,某市组织了一批年龄在[20,45]岁的志愿者为市民展开宣传活动,现从这批志愿者中随机抽取100名按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45],各组人数的频率分布直方图如图所示,现从第3,4,5组中用分层抽样的方法抽取6名志愿者参加宣传活动.分析 (Ⅰ)先分别求出这3组的人数,再利用分层抽样的方法即可得出答案;
(Ⅱ)从5名志愿者中抽取2名志愿者有10种情况,其中第4组的2名志愿者B1,B2至少有一名志愿者被抽中有7种情况,再利用古典概型的概率计算公式即可得出
解答 解:(Ⅰ) 第3组的人数为0.3×100=30,第4组的人数为0.2×100=20,第5组的人数为0.1×100=10.
因为第3,4,5组共有60名志愿者,
所以利用分层抽样的方法在60名志愿者中抽取6名志愿者,
每组抽取的人数分别为:第3组:$\frac{30}{60}$×6=3; 第4组:$\frac{20}{60}$×6=2; 第5组:$\frac{10}{60}$×6=1.
所以应从第3,4,5组中分别抽取3人,2人,1人;
(Ⅱ) 记第3组的3名志愿者为A1,A2,A3,第4组的2名志愿者为B1,B2,.则从5名志愿者中抽取2名志愿者有:
(A1,A2),(A1,A3),(A1,B1),(A1,B2),
(A2,A3),(A2,B1),(A2,B2),
(A3,B1),(A3,B2),(B1,B2)共有10种.
其中第4组的2名志愿者B1,B2至少有一名志愿者被抽中的有:
(A1,B1),(A1,B2),(A2,B1),(A2,B2),
(A3,B1),(A3,B2),(B1,B2),共有7种
所以第4组至少有一名志愿者被抽中的概率为$\frac{7}{10}$
点评 熟练掌握频率分布直方图、分层抽样的定义、古典概型的概率计算公式、互斥事件及相互独立事件的概率计算公式是解题的关键


科目:高中数学 来源: 题型:解答题
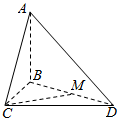 如图,已知AB⊥平面BCD,BC⊥CD,AD与平面BCD所成的角为30°,且AB=BC=2;
如图,已知AB⊥平面BCD,BC⊥CD,AD与平面BCD所成的角为30°,且AB=BC=2;查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 2 | C. | -1或2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com