
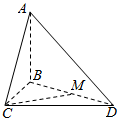
 如图,已知AB⊥平面BCD,BC⊥CD,AD与平面BCD所成的角为30°,且AB=BC=2;
如图,已知AB⊥平面BCD,BC⊥CD,AD与平面BCD所成的角为30°,且AB=BC=2;分析 (1)由AB⊥平面BCD,得CD⊥平面ABC,由此能求出三棱锥A-BCD的体积.
(2)以C为原点,CD为x轴,CB为y轴,过C作平面BCD的垂线为z轴,建立空间直角坐标系,由此能求出异面直线AD与CM所成角的大小.
解答 解:(1)如图,因为AB⊥平面BCD,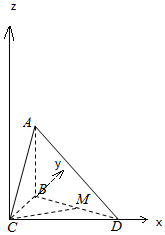
所以AB⊥CD,又BC⊥CD,所以CD⊥平面ABC,
因为AB⊥平面BCD,AD与平面BCD所成的角为30°,故∠ADB=30°,
由AB=BC=2,得AD=4,AC=2$\sqrt{2}$,
∴BD=$\sqrt{16-4}$=2$\sqrt{3}$,CD=$\sqrt{(2\sqrt{3})^{2}-{2}^{2}}$=2$\sqrt{2}$,
则VA-BCD=$\frac{1}{3}×{S}_{△BCD}×AB$=$\frac{1}{6}×BC×CD×AB$=$\frac{1}{6}×2×2\sqrt{2}×2$
=$\frac{4\sqrt{2}}{3}$.
(2)以C为原点,CD为x轴,CB为y轴,过C作平面BCD的垂线为z轴,
建立空间直角坐标系,
则A(0,2,2),D(2$\sqrt{2}$,0,0),C(0,0,0),B(0,2,0),M($\sqrt{2},1,0$),
$\overrightarrow{AD}$=(2$\sqrt{2}$,-2,-2),$\overrightarrow{CM}$=($\sqrt{2},1,0$),
设异面直线AD与CM所成角为θ,
则cosθ=$\frac{|\overrightarrow{AD}•\overrightarrow{CM}|}{|\overrightarrow{AD}|•|\overrightarrow{CM}|}$=$\frac{2}{4\sqrt{3}}$=$\frac{\sqrt{3}}{6}$.
θ=arccos$\frac{\sqrt{3}}{6}$.
∴异面直线AD与CM所成角的大小为arccos$\frac{\sqrt{3}}{6}$.
点评 本题考查了直线和平面所成角的计算,考查了利用等积法求点到面的距离,变换椎体的顶点,利用其体积相等求空间中点到面的距离是较有效的方法,此题是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{6}$个单位 | ||
| C. | 向左平移$\frac{π}{12}$个单位 | D. | 向右平移$\frac{π}{12}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | P=Q | B. | Q?P | C. | P∩Q={2,4} | D. | P∩Q={(2,4)} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某市为增强市民的环境保护意识,某市组织了一批年龄在[20,45]岁的志愿者为市民展开宣传活动,现从这批志愿者中随机抽取100名按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45],各组人数的频率分布直方图如图所示,现从第3,4,5组中用分层抽样的方法抽取6名志愿者参加宣传活动.
某市为增强市民的环境保护意识,某市组织了一批年龄在[20,45]岁的志愿者为市民展开宣传活动,现从这批志愿者中随机抽取100名按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45],各组人数的频率分布直方图如图所示,现从第3,4,5组中用分层抽样的方法抽取6名志愿者参加宣传活动.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | 0 | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com