
分析 (1)①先化简,再根据导数的运算法则计算即可,
②直接根据导数的运算法则求导即可,
(2)先根据导数的运算法则求导,再比较,即可得到函数g(x)的解析式.
解答 解:(1)①f(x)=(1-x)(1+x)(1+x2)(1+x4)=1-x16,则f′(x)=-16x15,
②f(x)=$\frac{2^x}{ln2}$,则f′(x)=2x,
(2)∵$f(x)=\frac{2sinx}{{1+{x^2}}}$,
∴f′(x)=$\frac{2}{(1+{x}^{2})^{2}}$•[cosx(1+x2)-2xsinx],
∴g(x)=cosx(1+x2)-2xsinx
点评 本题考查了导数的运算法则,关键时掌握基本求导公式,属于基础题.


科目:高中数学 来源: 题型:选择题
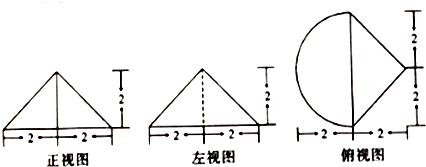
| A. | 4π+8 | B. | $4π+\frac{8}{3}$ | C. | $\frac{4π}{3}+8$ | D. | $\frac{4π+8}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com