
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{4}$ |
分析 由于过直角顶点C在∠ACB内部任作一射线CM,故可以认为所有可能结果的区域为∠ACB,可将事件A构成的区域为∠ACC',以角度为“测度”来计
解答 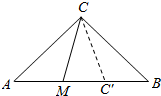 解:在AB上取AC'=AC,则∠ACC′=$\frac{180°-45°}{2}$=67.5°.
解:在AB上取AC'=AC,则∠ACC′=$\frac{180°-45°}{2}$=67.5°.
记A={在∠ACB内部任作一射线CM,与线段AB交于点M,AM<AC},
则所有可能结果的区域为∠ACB,
事件A构成的区域为∠ACC'.
又∠ACB=90°,∠ACC'=67.5°.
∴P(A)=$\frac{67.5°}{90°}$=$\frac{3}{4}$.
故选:C.
点评 本题考查了几何概型的概率求法;在利用几何概型的概率公式来求其概率时,几何“测度”可以是长度、面积、体积、角度等.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com