
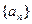 满足
满足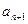 ≤
≤ . (1)若
. (1)若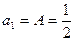 ,
,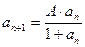 时,求
时,求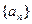 的通项公式; (2)若
的通项公式; (2)若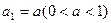 ,A=1,证明:
,A=1,证明: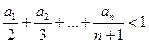
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
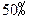 .每年年底扣除下一年的消费基金后,余下的资金投入再生产.这家牛奶厂每年应扣除多少消费基金,才能实现经过5年资金达到2000万元的目标?
.每年年底扣除下一年的消费基金后,余下的资金投入再生产.这家牛奶厂每年应扣除多少消费基金,才能实现经过5年资金达到2000万元的目标?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.0 | B.37 | C.100 | D.-37 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com