
【题目】已知数列![]() 的满足
的满足![]() ,前
,前![]() 项的和为
项的和为![]() ,且
,且![]() .
.
(1)求![]() 的值;
的值;
(2)设![]() ,证明:数列
,证明:数列![]() 是等差数列;
是等差数列;
(3)设![]() ,若
,若![]() ,求对所有的正整数
,求对所有的正整数![]() 都有
都有![]() 成立的
成立的![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() .
.
【解析】试题分析:(1)令![]() 得
得![]() (2) 因为
(2) 因为![]() ,所以
,所以![]() ①.所以
①.所以![]() ②,由②-①,得
②,由②-①,得![]() .因为
.因为![]() ,所以
,所以![]() .所以
.所以![]() ,即
,即![]() ,
,
即![]() 即可得证(3)由(2)知,因为
即可得证(3)由(2)知,因为![]() ,所以数列
,所以数列![]() 的通项公式为
的通项公式为![]() .因为
.因为![]() ,所以
,所以![]() ,所以
,所以![]() ,所以数列
,所以数列![]() 是常数列. 由
是常数列. 由![]() ,所以
,所以![]() .所以
.所以![]() .研究数列
.研究数列![]() 的单调性求出最小值,变量分离
的单调性求出最小值,变量分离![]() 即可得解.
即可得解.
试题解析:
(1)令![]() 得
得![]() .
.
(2)因为![]() ,所以
,所以![]() ①.
①.
所以![]() ②,
②,
由②-①,得![]() .
.
因为![]() ,所以
,所以![]() .
.
所以![]() ,即
,即![]() ,
,
即![]() ,所以数列
,所以数列![]() 是公差为1的等差数列.
是公差为1的等差数列.
(3)由(2)知,因为![]() ,所以数列
,所以数列![]() 的通项公式为
的通项公式为![]() .
.
因为![]() ,所以
,所以![]() ,
,
所以![]() ,所以数列
,所以数列![]() 是常数列.
是常数列.
由![]() ,所以
,所以![]() .
.
所以![]() .
.
因为![]()
所以数列![]() 为单调递增数列
为单调递增数列
当![]() 时,
时, ![]() ,即
,即![]() 的最小值为
的最小值为![]()
由![]() ,所以
,所以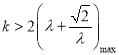 ,
,
而当![]() 时,
时, ![]() 在
在![]() 递减,
递减, ![]() 递增,所以
递增,所以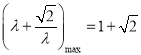 ,
,
当且仅当![]() 或
或![]() 时取得,故
时取得,故![]() .
.


科目:高中数学 来源: 题型:
【题目】[选修4-4,坐标系与参数方程]
在平面直角坐标系![]() 中,曲线C的参数方程为
中,曲线C的参数方程为![]()
![]() ,以坐标原点为极点,以
,以坐标原点为极点,以![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() 。
。
(1)求直线![]() 的直角坐标方程和曲线C的普通方程。
的直角坐标方程和曲线C的普通方程。
(2)设点P为曲线C上的任意一点,求点P到直线![]() 的距离的最大值。
的距离的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,以O为极点,x轴的正半轴为极轴建立极坐标系.若直线l的极坐标方程为![]() ,曲线C的极坐标方程为:
,曲线C的极坐标方程为: ![]() ,将曲线C上所有点的横坐标缩短为原来的一半,纵坐标不变,然后再向右平移一个单位得到曲线C1.
,将曲线C上所有点的横坐标缩短为原来的一半,纵坐标不变,然后再向右平移一个单位得到曲线C1.
(1)求曲线C1的直角坐标方程;
(2)已知直线l与曲线C1交于A,B两点,点P(2,0),求|PA|+|PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某县政府为了引导居民合理用水,决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价:若用水量不超过12吨时,按4元/吨计算水费;若用水量超过12吨且不超过14吨时,超过12吨部分按6.60元/吨计算水费;若用水量超过14吨时,超过14吨部分按7.80元/吨计算水费.为了了解全市居民月用水量的分布情况,通过抽样,获得了100户居民的月用水量(单位:吨),将数据按照![]() ,
,![]() ,…,
,…,![]() 分成8组,制成了如图1所示的频率分布直方图.
分成8组,制成了如图1所示的频率分布直方图.
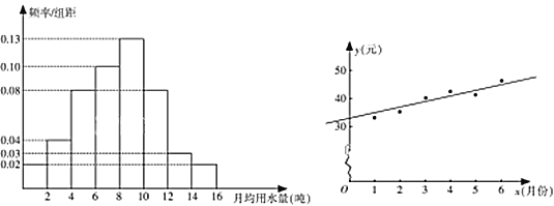
(图1) (图2)
(Ⅰ)通过频率分布直方图,估计该市居民每月的用水量的平均数和中位数(精确到0.01);
(Ⅱ)求用户用水费用![]() (元)关于月用水量
(元)关于月用水量![]() (吨)的函数关系式;
(吨)的函数关系式;
(Ⅲ)如图2是该县居民李某2017年1~6月份的月用水费![]() (元)与月份
(元)与月份![]() 的散点图,其拟合的线性回归方程是
的散点图,其拟合的线性回归方程是![]() .若李某2017年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
.若李某2017年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018江西莲塘一中、临川二中高三上学期第一次联考】二次函数![]() 的图象过原点,对
的图象过原点,对![]() ,恒有
,恒有![]() 成立,设数列
成立,设数列![]() 满足
满足![]() .
.
(I)求证:对![]() ,恒有
,恒有![]() 成立;
成立;
(II)求函数![]() 的表达式;
的表达式;
(III)设数列![]() 前
前![]() 项和为
项和为![]() ,求
,求![]() 的值.
的值.
【答案】(I)证明见解析;(II)![]() ;(III)2018.
;(III)2018.
【解析】试题分析:
(1)左右两侧做差,结合代数式的性质可证得![]() ,即对
,即对![]() ,恒有:
,恒有:![]() 成立;
成立;
(2)由已知条件可设![]() ,给定特殊值,令
,给定特殊值,令![]() ,从而可得:
,从而可得:![]() ,则
,则![]() ,
,![]() ,从而有
,从而有![]() 恒成立,据此可知
恒成立,据此可知![]() ,则
,则![]() .
.
(3)结合(1)(2)的结论整理计算可得:![]() ,据此分组求和有:
,据此分组求和有:![]() .
.
试题解析:
(1)![]() (仅当
(仅当![]() 时,取“=”)
时,取“=”)
所以恒有:![]() 成立;
成立;
(2)由已知条件可设![]() ,则
,则![]() 中,令
中,令![]() ,
,
从而可得:![]() ,所以
,所以![]() ,即
,即![]() ,
,
又因为![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
当![]() 时,
时,![]() ,不合题意舍去,
,不合题意舍去,
当![]() 时,即
时,即![]() ,所以
,所以![]() ,所以
,所以![]() .
.
(3)![]() ,
,
所以![]() ,
,
即![]() .
.
【题型】解答题
【结束】
22
【题目】已知函数![]() 为定义在
为定义在![]() 上的奇函数.
上的奇函数.
(1)求函数![]() 的值域;
的值域;
(2)当![]() 时,不等式
时,不等式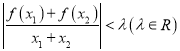 恒成立,求实数
恒成立,求实数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,AC=BC,M,N分别是棱CC1,AB的中点.
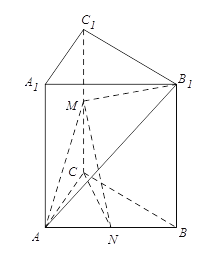
(1)求证:CN⊥平面ABB1A1;
(2)求证:CN∥平面AMB1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 中,
中, ![]() ,且
,且![]() 对任意正整数
对任意正整数![]() 都成立,数列
都成立,数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)若![]() ,且
,且![]() ,求
,求![]() ;
;
(2)是否存在实数![]() ,使数列
,使数列![]() 是公比为1的等比数列,且任意相邻三项
是公比为1的等比数列,且任意相邻三项![]() 按某顺序排列后成等差数列,若存在,求出所有
按某顺序排列后成等差数列,若存在,求出所有![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)若![]() ,求
,求![]() .(用
.(用![]() 表示).
表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() (m,n为常数),在
(m,n为常数),在![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅰ)求![]() 的解析式并写出定义域;
的解析式并写出定义域;
(Ⅱ)若任意![]() ,使得对任意
,使得对任意![]() 上恒有
上恒有![]() 成立,求实数a的取值范围;
成立,求实数a的取值范围;
(Ⅲ)若![]() 有两个不同的零点
有两个不同的零点![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com