
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
分析 设等比数列{an}的公比为q,则“a2>a1”?a1(q-1)>0?$\left\{\begin{array}{l}{{a}_{1}>0}\\{q>1}\end{array}\right.$,或$\left\{\begin{array}{l}{{a}_{1}<0}\\{q<1(q≠0)}\end{array}\right.$.由数列{an}为递增数列,可得$\left\{\begin{array}{l}{{a}_{1}>0}\\{q>1}\end{array}\right.$,或$\left\{\begin{array}{l}{{a}_{1}<0}\\{0<q<1}\end{array}\right.$.即可判断出结论.
解答 解:设等比数列{an}的公比为q,则“a2>a1”?a1(q-1)>0,?$\left\{\begin{array}{l}{{a}_{1}>0}\\{q>1}\end{array}\right.$,或$\left\{\begin{array}{l}{{a}_{1}<0}\\{q<1(q≠0)}\end{array}\right.$.
由数列{an}为递增数列,可得$\left\{\begin{array}{l}{{a}_{1}>0}\\{q>1}\end{array}\right.$,或$\left\{\begin{array}{l}{{a}_{1}<0}\\{0<q<1}\end{array}\right.$.
∴“a2>a1”是“数列{an}为递增数列”的必要不充分条件.
故选:B.
点评 本题考查了不等式的解法、等比数列的通项公式与单调性、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图1,在边长为2的菱形ABCD中,∠BAD=60°,将△BCD沿对角线BD折起到△B'CD的位置,使平面BC'D⊥平面ABD,E是BD的中点,FA⊥平面ABD,且FA=2$\sqrt{3}$,如图2.
如图1,在边长为2的菱形ABCD中,∠BAD=60°,将△BCD沿对角线BD折起到△B'CD的位置,使平面BC'D⊥平面ABD,E是BD的中点,FA⊥平面ABD,且FA=2$\sqrt{3}$,如图2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 贷款期限 | 6个月 | 12个月 | 18个月 | 24个月 | 36个月 |
| 频数 | 20 | 40 | 20 | 10 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
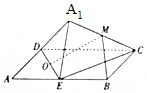 如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1∉平面ABCD),若M、O分别为线段A1C、DE的中点,则在△ADE翻转过程中,下列说法错误的是( )
如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1∉平面ABCD),若M、O分别为线段A1C、DE的中点,则在△ADE翻转过程中,下列说法错误的是( )| A. | 与平面A1DE垂直的直线必与直线BM垂直 | |
| B. | 异面直线BM与A1E所成角是定值 | |
| C. | 一定存在某个位置,使DE⊥MO | |
| D. | 三棱锥A1-ADE外接球半径与棱AD的长之比为定值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com