
【题目】已知正项数列{an}的前n项和为Sn , 点(an , Sn)(n∈N*)都在函数f(x)= ![]() 的图象上.
的图象上.
(1)求数列{an}的通项公式;
(2)若bn=an3n , 求数列{bn}的前n项和Tn .
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)写出曲线![]() 的参数方程和直线
的参数方程和直线![]() 的普通方程;
的普通方程;
(2)已知点![]() 是曲线
是曲线![]() 上一点,求点
上一点,求点![]() 到直线
到直线![]() 的最小距离.
的最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中的“两鼠穿墙题”是我国数学的古典名题:“今有垣厚若干尺,两鼠对穿,大鼠日一尺,小鼠也日一尺,大鼠日自倍,小鼠日自半,问何日相逢,各穿几何?”题意是:“有两只老鼠从墙的两边打洞穿墙,大老鼠第一天进一尺,以后每天加倍;小老鼠第一天也进一尺,以后每天减半.”如果墙足够厚,Sn为前n天两只老鼠打洞长度之和,则Sn=尺.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,定点
,定点![]() 为圆上一动点,线段
为圆上一动点,线段![]() 的垂直平分线交线段
的垂直平分线交线段![]() 于点
于点![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() ;
;
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)若经过![]() 的直线
的直线![]() 交曲线于不同的两点
交曲线于不同的两点![]() ,(点
,(点![]() 在点
在点![]() ,
, ![]() 之间),且满足
之间),且满足![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点B是以AC为直径的圆周上的一点,PA=AB=BC,AC=4,PA⊥平面ABC,点E为PB中点. 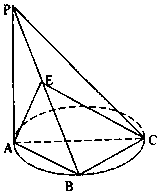
(Ⅰ)求证:平面AEC⊥平面PBC;
(Ⅱ)求直线AE与平面PAC所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,△ACD是边长为1的等边三角形,△ABC是等腰直角三角形,∠ACB=90°,BD交AC于点E. 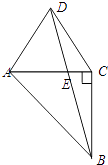
(1)求BD2的值;
(2)求线段AE的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表
商店名称 | A | B | C | D | E |
销售额x(千万元) | 3 | 5 | 6 | 7 | 9 |
利润额y(百万元) | 2 | 3 | 3 | 4 | 5 |
(1)画出散点图.观察散点图,说明两个变量有怎样的相关性.
(2)用最小二乘法计算利润额y对销售额x的回归直线方程.
(3)当销售额为4(千万元)时,估计利润额的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com