练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表

    商店名称

    A

    B

    C

    D

    E

    销售额x（千万元）

    3

    5

    6

    7

    9

    利润额y（百万元）

    2

    3

    3

    4

    5


    （1）画出散点图．观察散点图，说明两个变量有怎样的相关性．
    （2）用最小二乘法计算利润额y对销售额x的回归直线方程．
    （3）当销售额为4（千万元）时，估计利润额的大小．

    【答案】
    （1）解：根据所给的五组数据，得到五个有序数对，在平面直角坐标系中画出点，得到散点图．

    散点图


    （2）解：设回归直线的方程是： ， ；

    ∴ =

    a=0.4

    ∴y对销售额x的回归直线方程为：y=0.5x+0.4


    （3）解：当销售额为4（千万元）时，利润额为： =2.4（百万元）
    【解析】（1）画出散点图如图；（2）先求出x，y的均值，再由公式 = ， = ﹣ 计算出系数的值，即可求出线性回归方程；（3）将零售店某月销售额为4千万元代入线性回归方程，计算出y的值，即为此月份该零售点的估计值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知正项数列{an}的前n项和为Sn ， 点（an ， Sn）（n∈N*）都在函数f（x）= 的图象上．
    （1）求数列{an}的通项公式；
    （2）若bn=an3n ， 求数列{bn}的前n项和Tn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱ABC﹣A1B1C1中，AC⊥BC，点D是AB的中点．求证：
    （1）AC⊥BC1；
    （2）AC1∥平面B1CD．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数的图象过原点,且在处取得极值,直线与曲线在原点处的切线互相垂直.

    （Ⅰ）求函数的解析式；

    （Ⅱ）若对任意实数的,恒有成立,求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

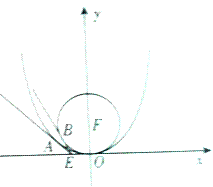
    【题目】如图所示，抛物线C：x2=2py（p＞0），其焦点为F，C上的一点M（4，m）满足|MF|=4．

    （1）求抛物线C的标准方程；

    （2）过点E（﹣1，0）作不经过原点的两条直线EA，EB分别与抛物线C和圆F：x2+（y﹣2）2=4相切于点A，B，试判断直线AB是否经过焦点F．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知不等式ax2+bx﹣1＜0的解集为{x|﹣1＜x＜2}．
    （1）计算a、b的值；
    （2）求解不等式x2﹣ax+b＞0的解集．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，边长为3的正方形所在平面与等腰直角三角形所在平面互相垂直， ，且， .

    （Ⅰ）求证： 平面；

    （Ⅱ）求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （l）求的单调区间；

    （2）若函数在区间内存在唯一的极值点，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱中， 是边长为4的正方形.平面⊥平面， .

    （1）求证： ⊥平面ABC；

    （2）求二面角的余弦值；

    （3）证明：在线段存在点，使得，并求的值.

    查看答案和解析>>

    同步练习册答案