
【题目】已知![]() ,
, ![]() .
.
(1)若![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 是
是![]() 成立的充分不必要条件,求实数
成立的充分不必要条件,求实数![]() 的取值范围.
的取值范围.
【答案】:(1)-2≤x≤8.(2)m≥6.
【解析】试题分析:
(1)求解一元二次不等式可得p为真命题时实数x的取值范围是-2≤x≤8;
(2)结合(1)的结论得到关于实数m的不等式组,求解不等式组可得实数m的取值范围是m≥6.
试题解析:
(1)由-x2+6x+16≥0,解得-2≤x≤8;
所以当p为真命题时,实数x的取值范围为-2≤x≤8.
(2)解法一:若q为真,可由x2-4x+4-m2≤0(m>0),解得2-m≤x≤2+m(m>0).
若p是q成立的充分不必要条件,则[-2,8]是[2-m,2+m]的真子集,
所以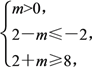 (两等号不同时成立),得m≥6.
(两等号不同时成立),得m≥6.
所以实数m的取值范围是m≥6.
解法二:设f(x)=x2-4x+4-m2(m>0),
若p是q成立的充分不必要条件,
∵x2-4x+4-m2≤0在[-2,8]恒成立,
则有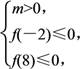 (两等号不同时成立),解得m≥6.
(两等号不同时成立),解得m≥6.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知p:关于x的不等式|x﹣2|+|x+2|>m的解集是R; q:关于x的不等式x2+mx+4>0的解集是R.则p成立是q成立的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.即不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
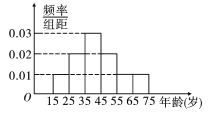
【题目】我市准备实施天然气价格阶梯制,现提前调查市民对天然气价格阶梯制的态度,随机抽查了50名市民,现将调查情况整理成了被调查者的频率分布直方图(如图)和赞成者的频数表如下:

(Ⅰ)若从年龄在![]() ,
,![]() 的被调查者中各随机选取2人进行调查,求所选取的4人中至少有2人对天然气价格阶梯制持赞成态度的概率;
的被调查者中各随机选取2人进行调查,求所选取的4人中至少有2人对天然气价格阶梯制持赞成态度的概率;
(Ⅱ)若从年龄在![]() ,
,![]() 的被调查者中各随机选取2人进行调查,记选取的4人中对天然气价格实施阶梯制持不赞成态度的人数为
的被调查者中各随机选取2人进行调查,记选取的4人中对天然气价格实施阶梯制持不赞成态度的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且a1+a5=17.
(1)若{an}还同时满足: ①{an}为等比数列;②a2a4=16;③对任意的正整数n,a2n<a2n+2 , 试求数列{an}的通项公式.
(2)若{an}为等差数列,且S8=56. ①求该等差数列的公差d;②设数列{bn}满足bn=3nan , 则当n为何值时,bn最大?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an}的前n项和为Sn , 点(an , Sn)(n∈N*)都在函数f(x)= ![]() 的图象上.
的图象上.
(1)求数列{an}的通项公式;
(2)若bn=an3n , 求数列{bn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com