
| A. | 19 | B. | 38 | C. | 18 | D. | 36 |
分析 根据抛物线的定义,到焦点的距离等于到准线的距离,求出A的坐标,而四边形ABEF为直角梯形,直角梯形的面积可求.
解答 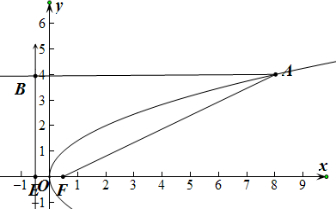 解:∵抛物线y2=2x的焦点为F,准线为l,
解:∵抛物线y2=2x的焦点为F,准线为l,
∴F($\frac{1}{2}$,1),准线l为x=-$\frac{1}{2}$,
∴|EF|=1,|AB|=|AF|,
设A(x0,y0),
∴|AB|=x0+$\frac{1}{2}$,
∵|AF|=$\frac{17}{2}$,
∴x0+$\frac{1}{2}$=$\frac{17}{2}$,
解得x0=8,
∴y02=2x0=16,
∴|y0|=4,
∴|BE|=|y0|=4,
∴S四边形ABEF=$\frac{1}{2}$(|EF|+|AB|)×|BE|=$\frac{1}{2}$(1+$\frac{17}{2}$)×4=19,
故选:A
点评 本题考查抛物线的定义、标准方程,以及简单性质的应用,判断四边形ABEF为直角梯形是解题的关键.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | 0 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com