
分析 根据题意,分2步进行分析:首先安排文科老师:先计算全部的安排方法数目,再排除其中不合题意的情况即可,其次安排理科老师:根据题意分析可得理科老师必须每人安排一天,由组合数公式计算可得其情况数目,进而由分步计数原理计算可得答案.
解答 解:根据题意,分2步进行分析:
首先安排文科老师:有23-2=6种安排方法,
其次安排理科老师:理科老师有6人,要求每天2人且每位老师至少答疑一天,至多答疑两天,
则必须每人安排一天,有$C_6^2C_4^2C_2^2$=90种安排方法;
则一共有6×90=540种安排方法,
答:不同的安排方法有540种.
点评 本题考查排列、组合的实际应用,注意理科老师有6人,要满足题意的话必须每人一天.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:选择题
| A. | 19 | B. | 38 | C. | 18 | D. | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 8 | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f′(a)<0,f′(b)<0 | B. | f′(a)>0,f′(b)>0 | C. | f′(a)<0,f′(b)>0 | D. | f′(a)>0,f′(b)<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (∁IM)∩(∁IN) | B. | (∁IM)∪(∁IN) | C. | M∪N | D. | M∩(∁IN) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{16}$ | D. | $\frac{1}{32}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
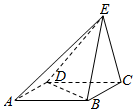 如图ABCD是平行四边形,已知AB=2BC=4,BD=2$\sqrt{3}$,BE=CE,平面BCE⊥平面ABCD.
如图ABCD是平行四边形,已知AB=2BC=4,BD=2$\sqrt{3}$,BE=CE,平面BCE⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com