
在直角坐标系 xOy 中,点 P 到两点 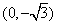 、
、 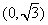 的距离之和等于4,设点 P 的轨迹为 C ,直线 y = kx +1与 C 交于 A 、 B 两点.
的距离之和等于4,设点 P 的轨迹为 C ,直线 y = kx +1与 C 交于 A 、 B 两点.
(1)写出 C 的方程;
(2)若 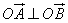 ,求 k 的值;
,求 k 的值;
(3)若点 A 在第一象限,证明当 k >0时,恒有 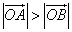 .
.
(1) 解: 设 P ( x , y ),由椭圆的定义可知,点 P 的轨迹 C 是以 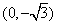 、
、 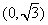 为焦点,长半轴为2的椭圆,它的短半轴
为焦点,长半轴为2的椭圆,它的短半轴 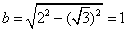 ,
,
故曲线 C 的方程为  .
.
(2) 解: 设 A ( x 1 , y 1 ), B ( x 2 , y 2 ),其坐标满足 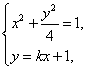
消去 y 并整理得( k 2 +4) x 2 +2 kx -3=0,
故 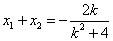 ,
, 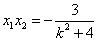
若 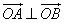 ,则 x 1 x 2 + y 1 y 2 =0.
,则 x 1 x 2 + y 1 y 2 =0.
而 y 1 y 2 = k 2 x 1 x 2 + k ( x 1 + x 2 )+1,
于是 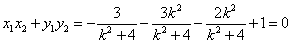 ,
,
化简得-4 k 2 +1=0,所以 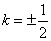 .
.
(3)证明: 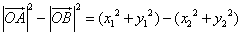

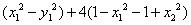
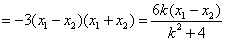 .
.
因为点 A 在第一象限,故 x 1 >0.
由 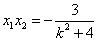 知 x 2 <0,
知 x 2 <0,
从而 x 1 - x 2 >0.
又 k >0,故 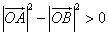 ,
,
即在题设条件下,恒有 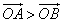 .
.


 中考解读考点精练系列答案
中考解读考点精练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com