练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    求函数f（x）=x2-2ax，x∈[0，4）的最小值．
    考点：二次函数在闭区间上的最值
    专题：函数的性质及应用
    分析：根据函数f（x）=（x-a）2-a2，x∈[0，4），分当a＜0时、当a∈[0，4）、当a≥4 时三种情况，分别求得函数的最小值．
    解答： 解：函数f（x）=x2-2ax=（x-a）2-a2，x∈[0，4），
    故当a＜0时，f（x）在[0，4）上是增函数，故函数的最小值为f（0）=0．
    当a∈[0，4）时，函数的最小值为f（a）=-a2．
    当a≥4 时，f（x）在[0，4）上是减函数，故函数无最小值．
    点评：本题主要考查求二次函数在闭区间上的最值，二次函数的性质的应用，体现了分类讨论的数学思想，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    某人忘记了自己的文档密码，但记得该密码是由一个2，一个9，两个6组成的四位数，于是用这四个数随意排成一个四位数，输入电脑尝试，那么他找到自己的文档密码最多尝试次数为（　　）
    A、36B、24C、18D、12

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=x2+（m-1）x+m，（m∈R+）
    （1）若f（x）是偶函数，求m的值．
    （2）设g（x）=
    f(x)
    x
    ，x∈[
    1
    4
    ，4]，求g（x）的最小值φ（m）．
    （3）若φ（m）-
    k
    4
    ＞log 
    1
    3
    427
    恒成立，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    AB是底部B是一个不可到达的建筑物，A为建筑物的最高点，设计一个方案测量AB的高度．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设等差数列{an}的前n项和为Sn，a4=S2，a2n+2=2an，
    （1）求数列{an}的通项公式；
    （2）若bn=
    4
    anan+1
    ，求数列{bn}的前n项和Tn，并求Tn的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    圆C的参数方程为
    x=2+cos∂
    y=3+sin∂
    （∂为参数），直线l的极坐标方程为ρsin（θ-
    π
    4
    ）=
    		2

    （1）求圆与直线的直角坐标方程；
    （2）直线l与圆C交于A、B，与x轴交于P，求PA+PB的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

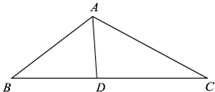    若可变形的三角形模型在变换过程中三角形周长和面积可同时取得最小值（或最大值），则称此模型为“周积三角形”．某模型厂家用一根定长连接杆AD，两根单向伸缩连接杆AB、AC（A端固定，B、C端可伸缩）以及一根双向伸缩连接杆BC制作了如图所示的可变三角形模型（所有连接杆均为笔直的金属杆）．模型中，双向伸缩杆BC用一个活动连接装置固定在D点，使BC可在D处自由转动．已知：模型中，∠BAD=∠CAD=60°，AD=1分米，AB和AC最多可伸长到5分米，BC的双向伸缩能力均很强．设AB=x分米，AC=y分米．
    （1）将y表示成x的函数，并求其定义域；
    （2）判断此模型是否为“周积三角形”模型，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=2cos2（x-
    π
    6
    ）+2sin（x-
    π
    4
    ）sin（x+
    π
    4
    ）-1．
    （1）求函数f（x）的最小正周期和单调递减区间；
    （2）求函数f（x）在区间[-
    π
    12
    ，
    π
    2
    ]上的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设数列{an}的前n项和Sn满足Sn=
    4
    3
    an-
    1
    3
    ×2n+1+
    2
    3
    （n∈N*），
    （Ⅰ）求a1及数列{an}的通项公式；
    （Ⅱ）记bn=
    2n
    Sn
    （n∈N*）证明：b1+b2+…+bn＜
    3
    2
    ．

    查看答案和解析>>

    同步练习册答案