考点:三角函数中的恒等变换应用,三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:(1)根据二倍角的正弦与余弦及辅助角公式,将解析式化为y=Asin(ωx+φ)+B的基本形式,根据正弦函数的性质,求出最小正周期和单调减区间;
(2)由x的范围求出“
2x-”的范围,根据正弦函数的单调性判断出函数的单调性,再求出端点处的函数值,进行比较后得函数的最值,即求出函数的值域.
解答:
解:(1)∵f(x)=2cos
2(x-
)+2sin(x-
)sin(x+
)-1
=
cos(2x-)+2sin(x-)sin(x+-)=
cos(2x-)+2sin(x-)cos(x-)=
cos2x+sin2x+sin(2x-)=
cos2x+sin2x-cos2x=
sin2x-cos2x=
sin(2x-)∴周期 T=π---------------------(6分)
由
+2kπ≤2x-≤+2kπ(k∈Z)得,
+kπ≤x≤+kπ(k∈Z)∴函数f(x)的单调递减区间为
[+kπ,+kπ](k∈Z)-------------(8分)
(2)∵x∈[-
,
],∴
2x-∈[-,],-----------(9分)
∵函数f(x)=
sin(2x-)在区间
[-,] 上单调递增,在区间
[,]上单调递减,
∴当x=
时,f(x)取最大值
f()=sin(-)=sin=1.
又∵
f(-)=sin(-)=
-,且
f()=sin(π-)=sin=
,
∴当x=-
时,f(x)取最小值
-.
∴函数f(x)在区间[-
,
]上的值域为
[-,1]------------------------(12分)
点评:本题考查了诱导公式、二倍角的正弦与余弦、辅助角公式的应用,正弦函数的周期性、利用正弦函数的单调性求给定区间上的值域问题,属于中档题.



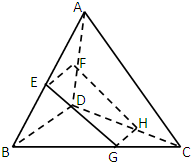 如图,已知空间四边形ABCD,E,F分别是AB,AD的中点,G,H分别是BC,CD上的点,且
如图,已知空间四边形ABCD,E,F分别是AB,AD的中点,G,H分别是BC,CD上的点,且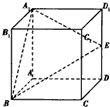 如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点.
如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点.