考点:二次函数的性质,对数的运算性质
专题:函数的性质及应用
分析:(1)根据二次函数f(x)的对称轴为x=0,求得m的值.
(2)求得g(x)x+(m-1)+
,分当m=0时、当m<0时、当m>0时三种情况,分别求得g(x)的最小值φ(m)的解析式,综合可得,g(x)的最小值φ(m)的解析式.
(3)由题意可得 φ(m)>
恒成立,再根据φ(m)的最小值为
,可得
>
,由此解得实数k的取值范围.
解答:
解:(1)若函数f(x)=x
2+(m-1)x+m为偶函数,则有
=0,解得m=1.
(2)∵g(x)=
=x+(m-1)+
,
当m=0时,g(x)=x
2,g(x)的最小值φ(m)=g(
)=
.
当m<0时,g(x)在[
,4]上是增函数,g(x)的最小值φ(m)=g(
)=
.
当m>0时,g(x)在[
,+∞)上是增函数,
若
≤m<2,g(x)的最小值φ(m)=2m;
若 m>2,g(x)在[
,4]上是减函数,g(x)的最小值φ(m)=g(4)=
+3;
若0<m<
,g(x)在[
,4]上是增函数,g(x)的最小值φ(m)=g(
)=
.
综上可得,g(x)的最小值φ(m)=
.
(3)若φ(m)-
>log
=
log3=-
恒成立,
∴φ(m)>
恒成立.
再根据φ(m)的最小值为
,∴
>
,解得 k<
.
即实数k的取值范围为(-∞,
).
点评:本题主要考查二次函数的性质,对数的运算性质,体现了分类讨论、转化的数学思想,属于基础题.



 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案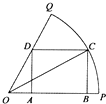 如图,已知OPQ是半径为
如图,已知OPQ是半径为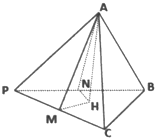 在三棱锥P-ABC中,PA=a,PB=b,PC=c,且∠BPC=α,∠APC=β,∠APB=γ.
在三棱锥P-ABC中,PA=a,PB=b,PC=c,且∠BPC=α,∠APC=β,∠APB=γ.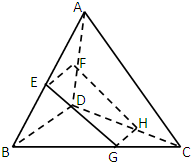 如图,已知空间四边形ABCD,E,F分别是AB,AD的中点,G,H分别是BC,CD上的点,且
如图,已知空间四边形ABCD,E,F分别是AB,AD的中点,G,H分别是BC,CD上的点,且