Question

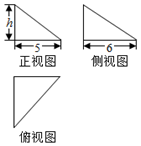
8．如图所示，三个直角三角形是一个体积为20cm³的几何体的三视图，则该几何体外接球的表面积（单位：cm²）等于（　　）

• A． 75π
• B． 77π
• C． 65π
• D． 55π

Answer 1

分析 作出几何体的三视图，建立空间坐标系，求出外接球的球心坐标，从而可得外接球的半径，进而求出外接球的表面积．

解答 解：作出三棱锥的三视图如图所示：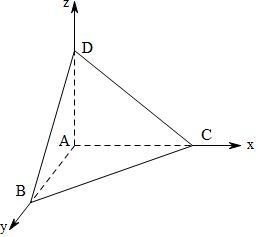

由三视图可知AB，AC，AD两两垂直，且AB=6，AC=5，AD=h，
∴V_D-ABC=$\frac{1}{3}×\frac{1}{2}×5×6×h$=20，∴h=4．
以A为原点，以AC，AB，AD为坐标轴建立空间直角坐标系，
则A（0，0，0），B（0，6，0），C（5，0，0），D（0，0，4）．
设三棱锥的外接球的球心为M（x，y，z），则MA=MB=MC=MD，
∴x²+y²+z²=x²+（y-6）²+z²=（x-5）²+y²+z²=x²+y²+（z-4）²，
解得x=$\frac{5}{2}$，y=3，z=2，
∴外接球的半径r=MA=$\sqrt{{x}^{2}+{y}^{2}+{z}^{2}}$=$\frac{\sqrt{77}}{2}$，
∴外接球的表面积S=4πr²=77π．
故选：B．

点评 本题考查了棱锥的三视图，棱锥的体积计算，球与棱锥的位置关系，属于中档题．