
【题目】已知定义在![]() 上的函数
上的函数![]() 满足:
满足:
①对于任意的![]() ,都有
,都有![]() ;
;
②当![]() 时,
时,![]() ,且
,且![]() .
.
(1)求![]() ,
,![]() 的值,并判断函数
的值,并判断函数![]() 的奇偶性;
的奇偶性;
(2)判断函数![]() 在
在![]() 上的单调性;
上的单调性;
(3)求函数![]() 在区间
在区间![]() 上的最大值.
上的最大值.
【答案】(1)![]() 为偶函数;(2)
为偶函数;(2)![]() 在
在![]() 上是增函数;(3)2.
上是增函数;(3)2.
【解析】
(1)先求f(﹣1)的值,令y=﹣1,推出f(﹣x)=f(x)+f(﹣1),f(﹣x)=f(x).结合函数奇偶性的定义,判断函数f(x)的奇偶性;
(2)利用函数单调性的定义,直接判断函数f(x)在(0,+∞)上的单调性;
(3)通过(1),(2)奇偶性,单调性,直接求函数f(x)在区间[﹣4,0)∪(0,4]上的最大值;
(1)令x=y=1,则f(1×1)=f(1)+f(1),得f(1)=0;
再令x=y=﹣1,则f[(﹣1)×(﹣1)]=f(﹣1)+f(﹣1),得f(﹣1)=0.
对于条件f(xy)=f(x)+f(y),令y=﹣1,
则f(﹣x)=f(x)+f(﹣1),所以f(﹣x)=f(x).
又函数f(x)的定义域关于原点对称,所以函数f(x)为偶函数.
(2)任取x1,x2∈(0,+∞),且x1<x2,则有![]() .
.
又∵当x>1时,f(x)>0,
∴f(![]() )>0
)>0
而![]() >f(x1),
>f(x1),
所以函数f(x)在(0,+∞)上是增函数.
(3)∵f(4)=f(2×2)=f(2)+f(2),又f(2)=1,
∴f(4)=2.
又由(1)知函数f(x)在区间[﹣4,0)∪(0,4]上是偶函数且在(0,4]上是增函数,
∴函数f(x)在区间[﹣4,0)∪(0,4]上的最大值为f(4)=f(﹣4)=2.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】某市为了创建全国文明城市,面向社会招募志愿者,现从20岁至50岁的志愿者中按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
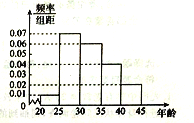
,第5组![]() ,得到的频率分布直方图如图所示,若用分层抽样的方法从这些志愿者中抽取20人参加“创建全国文明城市验收日”的活动。
,得到的频率分布直方图如图所示,若用分层抽样的方法从这些志愿者中抽取20人参加“创建全国文明城市验收日”的活动。
(1)求从第2组和第3组中抽取的人数分别是多少;
(2)若小李和小王都是32岁,同时参加了“创建全国文明城市验收日”的活动,现要从第3组抽取的人中临时抽调两人去执行另一任务,求小李和小王至少有一人被抽调的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出函数![]() 如下表,则f〔g(x)〕的值域为( )
如下表,则f〔g(x)〕的值域为( )
x | 1 | 2 | 3 | 4 |
g(x) | 1 | 1 | 3 | 3 |
x | 1 | 2 | 3 | 4 |
f(x) | 4 | 3 | 2 | 1 |
A. {4,2} B. {1,3} C. {1,2,3,4} D. 以上情况都有可能
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,角A,B,C所对的边分别为a,b,c,( ![]() a﹣sinC)cosB=sinBcosC,b=4
a﹣sinC)cosB=sinBcosC,b=4 ![]() .
. 
(1)求角B的大小;
(2)D为BC边上一点,若AD=2,S△DAC=2 ![]() ,求DC的长.
,求DC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() ,直线
,直线![]() ,设圆
,设圆![]() 的半径为
的半径为![]() ,且圆心
,且圆心![]() 在直线
在直线![]() 上.
上.
(![]() )若圆心
)若圆心![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作圆
作圆![]() 的切线,求切线的方程.
的切线,求切线的方程.
(![]() )若圆
)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4﹣5:不等式选讲
已知函数f(x)=|x﹣2|﹣|x﹣5|.
(1)证明:﹣3≤f(x)≤3;
(2)求不等式f(x)≥x2﹣8x+15的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(Rt△FHE,H是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上.已知AB=20米,AD=10 ![]() 米,记∠BHE=θ.
米,记∠BHE=θ. 
(1)试将污水净化管道的长度L表示为θ的函数,并写出定义域;
(2)问:当θ取何值时,污水净化效果最好?并求出此时管道的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com