Question

14．已知△ABC是等腰直角三角形．|$\overrightarrow{AB}$|=|$\overrightarrow{AC}$|=1，$\overrightarrow{BC}$=4$\overrightarrow{BD}$，
（1）求$\overrightarrow{AD}$•（$\overrightarrow{AB}$-$\overrightarrow{AC}$）
（2）若点M在线段BC上，求$\overrightarrow{AM}$•$\overrightarrow{MD}$的最大值．

Answer 1

分析 （1）根据向量数量积的公式进行转化求解即可．
（2）建立坐标系，将三角形放入坐标系，求出B，C，D，M的坐标，利用向量共线定理转化为关于λ的一元二次函数进行求解即可．

解答 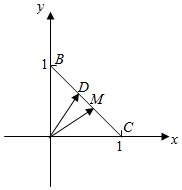解：（1）$\overrightarrow{AD}$•（$\overrightarrow{AB}$-$\overrightarrow{AC}$）=（$\overrightarrow{AB}$+$\overrightarrow{BD}$）•$\overrightarrow{CB}$
=（$\overrightarrow{AB}$+$\frac{1}{4}$$\overrightarrow{BC}$）•$\overrightarrow{CB}$=$\overrightarrow{AB}$$•\overrightarrow{CB}$-$\frac{1}{4}$$\overrightarrow{BC}$²=1×$\sqrt{2}×$cos45°-$\frac{1}{4}×（\sqrt{2}）^{2}$=$\frac{\sqrt{2}}{2}×\sqrt{2}$-$\frac{1}{4}×2$=1-$\frac{1}{2}=\frac{1}{2}$．
（2）将直角三角形放入坐标系中，
则A（0，0），B（0，1），C（1，0），
$\overrightarrow{BC}$=4$\overrightarrow{BD}$=（1，-1），
 则4（x，y-1）=（1，-1），
则$\left\{\begin{array}{l}{4x=1}\\{4（y-1）=-1}\end{array}\right.$，则$\left\{\begin{array}{l}{x=\frac{1}{4}}\\{y=\frac{3}{4}}\end{array}\right.$，即D（$\frac{1}{4}$，$\frac{3}{4}$），
∵点M在线段BC，∴设$\overrightarrow{BM}$=λ$\overrightarrow{BC}$=（λ，-λ），0≤λ≤1，
则M（λ，1-λ），
则$\overrightarrow{AM}$•$\overrightarrow{MD}$=（λ，1-λ）•（$\frac{1}{4}$-λ，λ-$\frac{1}{4}$）=（$\frac{1}{4}$-λ）λ+（1-λ）（λ-$\frac{1}{4}$）=-2λ²+$\frac{3}{2}$λ-$\frac{1}{4}$
=-2（λ-$\frac{3}{8}$）²+$\frac{1}{32}$，
故当λ=$\frac{3}{8}$时，$\overrightarrow{AM}$•$\overrightarrow{MD}$取得最大值$\frac{1}{32}$．

点评 本题主要考查向量数量积的应用，根据向量数量积的定义以及建立坐标系，利用坐标法是解决本题的关键．