
分析 将曲线C2的参数方程代入曲线C1的方程,可得t=1,再由x=ρcosθ,y=ρsinθ,tanθ=$\frac{y}{x}$,求得ρ,θ,即可得到所求坐标.
解答 解:将曲线C2的参数方程$\left\{\begin{array}{l}{x=2-t}\\{y=t}\end{array}\right.$(t为参数)代入
曲线C1的方程为x2+y2=2,可得
(2-t)2+t2=2,
解得t=1,
可得交点的直角坐标为(1,1),
由x=ρcosθ,y=ρsinθ,tanθ=$\frac{y}{x}$,
可得ρ=$\sqrt{1+1}$=$\sqrt{2}$,tanθ=1,0<θ<$\frac{π}{2}$,
可得θ=$\frac{π}{4}$.
可得交点的极坐标为($\sqrt{2}$,$\frac{π}{4}$).
故答案为:($\sqrt{2}$,$\frac{π}{4}$).
点评 本题考查极坐标与直角坐标的互化,考查联立两曲线方程求交点,考查运算能力,属于基础题.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | ($\frac{1}{e}$,e) | C. | ($\frac{1}{4}$,e) | D. | ($\frac{1}{4}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PA⊥底面ABCD,M、N分别为PD、AC的中点.
在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PA⊥底面ABCD,M、N分别为PD、AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
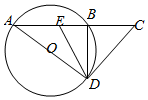 如图,A,B是圆O上两点,延长AB至点C,满足AB=2BC=2,过C作直线CD与圆O相切于点D,∠ADB的平分线交AB于点E.
如图,A,B是圆O上两点,延长AB至点C,满足AB=2BC=2,过C作直线CD与圆O相切于点D,∠ADB的平分线交AB于点E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | log2(-m)>log2n | B. | $\frac{n}{m^3}<\frac{1}{n}$ | C. | |m|<|n| | D. | $\root{3}{m}>\root{3}{n}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com