
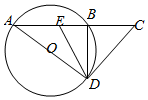
 如图,A,B是圆O上两点,延长AB至点C,满足AB=2BC=2,过C作直线CD与圆O相切于点D,∠ADB的平分线交AB于点E.
如图,A,B是圆O上两点,延长AB至点C,满足AB=2BC=2,过C作直线CD与圆O相切于点D,∠ADB的平分线交AB于点E.分析 (I)由圆的弦切角定理和切割线定理,以及内角平分线的定义,计算即可得到所求AE的长;
(11)由两角对应相等,可得△CDB∽△CAD,即有对应边成比例,结合三角形的余弦定理和面积公式,计算即可得到所求面积.
解答 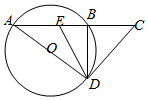 解:(I)由题可知∠CDB=∠DAB,∠EDA=∠EDB,
解:(I)由题可知∠CDB=∠DAB,∠EDA=∠EDB,
又∠CED=∠DAE+∠EDA,∠EDC=∠EDB+∠BDC
故∠CED=∠EDC,故CD=CE,
由AB=2BC=2,即有BC=1,AC=3,
可得CD2=CB•CA=3,即$CD=\sqrt{3}$,故$C{E}=\sqrt{3}$,
故AE的长为AC-CE=$3-\sqrt{3}$;
(11)因为直线CD与圆O相切于点D,
则∠CDB=∠DAC,则△CDB∽△CAD,
则$\frac{{{B}D}}{{{A}D}}=\frac{CD}{{{A}C}}=\frac{{\sqrt{3}}}{3}⇒{A}D=\sqrt{3}{B}D$,
设BD=m,${A}D=\sqrt{3}m$,
△ABD中,由余弦定理得3m2=m2+4-4mcos60°,
解之得m=1,由(I)知${B}{E}=\sqrt{3}-1$,
故所求△BDE的面积为$\frac{1}{2}$BE•BD•sin60°=$\frac{1}{2}({\sqrt{3}-1})•1•\frac{{\sqrt{3}}}{2}=\frac{{3-\sqrt{3}}}{4}$.
点评 本题考查圆的弦切角定理和切割线定理、相似三角形的判定和性质及三角形的余弦定理和面积公式的运用,考查推理和运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}x=2x'\\ y=3y'\end{array}\right.$ | B. | .$\left\{\begin{array}{l}x=\frac{1}{2}x'\\ y=\frac{1}{3}y'\end{array}\right.$ | C. | .$\left\{\begin{array}{l}x=4x'\\ y=9y'\end{array}\right.$ | D. | .$\left\{\begin{array}{l}x=\frac{1}{4}x'\\ y=\frac{1}{9}y'\end{array}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-3x+1 | B. | y=|x+2| | C. | y=$\frac{4}{x}$ | D. | y=x2-4x+3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com