
【题目】已知椭圆C的中心在原点,焦点在x轴上,离心率为![]() ,它的一个顶点恰好是抛物线x2=4
,它的一个顶点恰好是抛物线x2=4![]() y的焦点.
y的焦点.
(1)求椭圆C的方程;
(2)直线x=2与椭圆交于P,Q两点,P点位于第一象限,A,B是椭圆上位于直线x=2两侧的动点.
①若直线AB的斜率为![]() ,求四边形APBQ面积的最大值;
,求四边形APBQ面积的最大值;
②当点A,B运动时,满足∠APQ=∠BPQ,问直线AB的斜率是否为定值,请说明理由.
【答案】(1)![]() ;(2)①
;(2)①![]() ②
②![]()
【解析】
(1)根据抛物线焦点,求得b,再由离心率和椭圆中a、b、c的关系求得a、c的值,进而得到椭圆的标准方程。
(2)设出A、B的坐标,联立直线与椭圆的方程,结合韦达定理求得x1+x2=-2t,x1x2=2t2-4;由直线x=2与椭圆交于P,Q两点可求得P,Q两点的坐标,则四边形APBQ的面积S=S△APQ+S△BPQ,即可得到面积的最大值;设出直线方程,联立椭圆方程,化简得到关于x的一元二次方程,利用韦达定理得到AB斜率的表达形式,即可得到斜率为定值。
(1)设椭圆C的方程为![]() =1(a>b>0),由题意可得它的一个顶点恰好是抛物线x2=4
=1(a>b>0),由题意可得它的一个顶点恰好是抛物线x2=4![]() y的焦点(0,
y的焦点(0,![]() ),∴b=
),∴b=![]() .
.
再根据离心率![]() ,求得a=2
,求得a=2![]() ,
,
∴椭圆C的方程为![]() =1.
=1.
(2)①设A(x1,y1),B(x2,y2),AB的方程为y=![]() x+t,代入椭圆C的方程化简可得x2+2tx+2t2-4=0,由Δ=4t2-4(2t2-4)>0,求得-2<t<2.
x+t,代入椭圆C的方程化简可得x2+2tx+2t2-4=0,由Δ=4t2-4(2t2-4)>0,求得-2<t<2.
由根与系数的关系可得x1+x2=-2t,x1x2=2t2-4.
在![]() =1中,令x=2求得P(2,1),Q(2,-1),
=1中,令x=2求得P(2,1),Q(2,-1),
∴四边形APBQ的面积S=S△APQ+S△BPQ=![]() ·PQ·|x1-x2|=
·PQ·|x1-x2|=![]() ×2×|x1-x2|=|x1-x2|=
×2×|x1-x2|=|x1-x2|=![]() ,
,
故当t=0时,四边形APBQ的面积S取得最大值为4.
②当∠APQ=∠BPQ时,PA,PB的斜率之和等于零,设PA的斜率为k,则PB的斜率为-k,PA的方程为y-1=k(x-2),把它代入椭圆C的方程化简可得(1+4k2)x2+8k(1-2k)x+4(1-2k)2-8=0,
∴x2+2=![]() .
.
同理可得直线PB的方程为y-1=-k(x-2),x2+2=![]() ,
,
∴x1+x2=![]() ,x1-x2=
,x1-x2=![]() .
.
∴AB的斜率k=![]()
=![]()
=![]()
=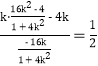 .
.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
【题目】朱世杰是历史上最伟大的数学家之一,他所著的《四元玉鉴》卷中“如像招数”五问中有如下问题:“今有官司差夫一千八百六十四人筑堤,只云初日差六十四人,次日转多七人,每人日支米三升”。其大意为“官府陆续派遣1864人前往修筑堤坝,第一天派出64人,从第二天开始每天派出的人数比前一天多7人,修筑堤坝的每人每天分发大米3升”,在该问题中第3天共分发大米( )
A. 192升 B. 213升 C. 234升 D. 255升
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知AB为半圆O的直径,AB=4,C为半圆上一点,过点C作半圆的切线CD,过点A作AD⊥CD于D,交半圆于点E,DE=1.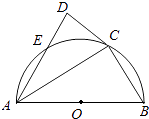
(1)求证:AC平分∠BAD;
(2)求BC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x3+ax2+bx+1的导数![]() 满足
满足![]() ,其中常数a,b∈R.
,其中常数a,b∈R.
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)设![]() ,求函数g(x)的极值.
,求函数g(x)的极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆O为△ABC的外接圆,过点C作圆O的切线交AB的延长线于点D,∠ADC的平分线交AC于点E,∠ACB的平分线交AD于点H. 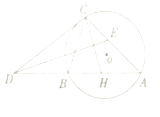
(1)求证:CH⊥DE;
(2)若AE=2CE.证明:DC=2DB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}为等差数列,前n项和为Sn(n∈N+),{bn}是首项为2的等比数列,且公比大于0,b2+b3=12,b3=a4﹣2a1 , S11=11b4 .
(Ⅰ)求{an}和{bn}的通项公式;
(Ⅱ)求数列{a2nb2n﹣1}的前n项和(n∈N+).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com