
【题目】设函数f(x)=x3+ax2+bx+1的导数![]() 满足
满足![]() ,其中常数a,b∈R.
,其中常数a,b∈R.
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)设![]() ,求函数g(x)的极值.
,求函数g(x)的极值.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)求出导函数f′(x)=3x2+2ax+b,利用约束条件列出方程,求出a,b,求出切点坐标以及斜率,然后求解切线方程;(2)化简g(x)=(3x2﹣3x﹣3)e﹣x,求出导数,求出极值点,判断导函数的符号,推出函数的单调性,求解函数的极值即可.
(1)∵f(x)=x3+ax2+bx+1,∴f′(x)=3x2+2ax+b,
则![]() 解得
解得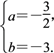
∴f(x)=x3-![]() x2-3x+1,∴f(1)=-
x2-3x+1,∴f(1)=-![]() ,f′(1)=-3,
,f′(1)=-3,
∴y=f(x)在(1,f(1))处的切线方程为
y-![]() =-3(x-1),即6x+2y-1=0;
=-3(x-1),即6x+2y-1=0;
(2)由(1)知g(x)=(3x2-3x-3)e-x,
∴g′(x)=(-3x2+9x)e-x,
令g′(x)=0,即(-3x2+9x)e-x=0,得x=0或x=3,
当x∈(-∞,0)时,g′(x)<0,
故g(x)在(-∞,0)上单调递减.
当x∈(0,3)时,g′(x)>0,故g(x)在(0,3)上单调递增.
当x∈(3,+∞)时,g′(x)<0,
故g(x)在(3,+∞)上单调递减.
从而函数g(x)在x=0处取得极小值g(0)=-3,
在x=3处取得极大值g(3)=15e-3.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案科目:高中数学 来源: 题型:
【题目】两台车床加工同一种机械零件如下表:
分类 | 合格品 | 次品 | 总计 |
第一台车床加工的零件数 | 35 | 5 | 40 |
第二台车床加工的零件数 | 50 | 10 | 60 |
总计 | 85 | 15 | 100 |
从这100个零件中任取一个零件,求:
(1)取得合格品的概率;
(2)取得零件是第一台车床加工的合格品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的镀锌铁皮材料ABCD,上沿DC为圆弧,其圆心为A,圆半径为2米,AD⊥AB,BC⊥AB,且BC=1米。现要用这块材料裁一个矩形PEAF(其中P在圆弧DC上、E在线段AB上,F在线段AD上)做圆柱的侧面,若以PE为母线,问如何裁剪可使圆柱的体积最大?其最大值是多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P是椭圆E:![]() +y2=1上的任意一点,F1,F2是它的两个焦点,O为坐标原点,动点Q满足
+y2=1上的任意一点,F1,F2是它的两个焦点,O为坐标原点,动点Q满足![]() .
.
(1)求动点Q的轨迹方程;
(2)若已知点A(0,-2),过点A作直线l与椭圆E相交于B,C两点,求△OBC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点F1(﹣c,0),F2(c,0)分别是椭圆C: ![]() =1(a>1)的左、右焦点,P为椭圆C上任意一点,且
=1(a>1)的左、右焦点,P为椭圆C上任意一点,且 ![]()
![]() 的最小值为0.
的最小值为0. 
(1)求椭圆C的方程;
(2)如图,动直线l:y=kx+m与椭圆C有且仅有一个公共点,点M,N是直线l上的两点,且F1M⊥l,F2N⊥l,求四边形F1MNF2面积S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知椭圆C:![]() 的离心率
的离心率![]() ,F1,F2分别为左、右焦点,过F1的直线交椭圆C于P,Q两点,且
,F1,F2分别为左、右焦点,过F1的直线交椭圆C于P,Q两点,且![]() 的周长为8.
的周长为8.
(1)求椭圆c的方程;
(2)设过点M(3,0)的直线交椭圆C于不同两点A,B,N为椭圆上一点,且满足![]() (O为坐标原点),当
(O为坐标原点),当![]() 时,求实数t的取值范围.
时,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在原点,焦点在x轴上,离心率为![]() ,它的一个顶点恰好是抛物线x2=4
,它的一个顶点恰好是抛物线x2=4![]() y的焦点.
y的焦点.
(1)求椭圆C的方程;
(2)直线x=2与椭圆交于P,Q两点,P点位于第一象限,A,B是椭圆上位于直线x=2两侧的动点.
①若直线AB的斜率为![]() ,求四边形APBQ面积的最大值;
,求四边形APBQ面积的最大值;
②当点A,B运动时,满足∠APQ=∠BPQ,问直线AB的斜率是否为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆![]() 的圆心在
的圆心在![]() 轴上,并且过
轴上,并且过![]() 两点.
两点.
(1)求圆![]() 的方程;
的方程;
(2)设直线![]() 与圆
与圆![]() 交于
交于![]() 两点,那么以
两点,那么以![]() 为直径的圆能否经过原点,若能,请求出直线
为直径的圆能否经过原点,若能,请求出直线![]() 的方程;若不能,请说明理由.
的方程;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),…[80,90],并整理得到如下频率分布直方图: 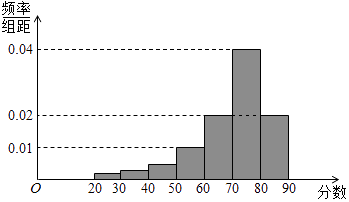
(Ⅰ)从总体的400名学生中随机抽取一人,估计其分数小于70的概率;
(Ⅱ)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(Ⅲ)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com