
【题目】已知点P是椭圆E:![]() +y2=1上的任意一点,F1,F2是它的两个焦点,O为坐标原点,动点Q满足
+y2=1上的任意一点,F1,F2是它的两个焦点,O为坐标原点,动点Q满足![]() .
.
(1)求动点Q的轨迹方程;
(2)若已知点A(0,-2),过点A作直线l与椭圆E相交于B,C两点,求△OBC面积的最大值.
【答案】(1)![]() ;(2)1
;(2)1
【解析】
(1)根据椭圆方程,写出两个焦点坐标;设出动点Q,根据向量的坐标运算,求出P与Q的关系,再根据P在椭圆上,进而求得动点Q的轨迹方程。
(2)首先根据题意可知直线的斜率必定存在,又因为过点A,可利用点斜式设出直线方程。联立椭圆,设出B(x1,y1),C(x2,y2)的坐标;利用判别式大于0,可求得k的取值范围;利用韦达定理表示出三角形OBC的面积,进而结合基本不等式可求得最后面积的最大值。
(1)∵a2=4,b2=1,∴c=![]() .
.
∴F1(-![]() ,0),F2(
,0),F2(![]() ,0).
,0).
设Q(x,y),P(x0,y0),
∵动点Q满足![]() ,
,
∴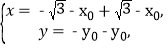
解得x0=-![]() ,y0=-
,y0=-![]() ,
,
又(x0,y0)在![]() +y2=1上,代入椭圆方程可得
+y2=1上,代入椭圆方程可得![]() =1,∴动点Q的轨迹方程为
=1,∴动点Q的轨迹方程为![]() =1.
=1.
(2)由题意可知:直线l的斜率存在,设直线l的方程为y=kx-2,B(x1,y1),C(x2,y2).
联立 整理得(1+4k2)x2-16kx+12=0.
整理得(1+4k2)x2-16kx+12=0.
由Δ>0,解得k2>![]() .
.
∴x1+x2=![]() ,x1x2=
,x1x2=![]() .
.
S△OBC=S△OAC-S△OAB=![]() |OA|·(|x2|-|x1|)=|x2-x1|=
|OA|·(|x2|-|x1|)=|x2-x1|=![]()
=![]() .
.
令![]() =t>0,化为4k2=t2+3.
=t>0,化为4k2=t2+3.
∴S△OBC=![]() =1,
=1,
当且仅当t=2时取等号,此时k=±![]() .
.
∴(S△OBC)max=1.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:
【题目】交通部门对某路段公路上行驶的汽车速度实施监控,从速度在50﹣90km/h的汽车中抽取150辆进行分析,得到数据的频率分布直方图如图所示,则速度在70km/h以下的汽车有辆.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由代数式的乘法法则类比推导向量的数量积的运算法则:
①“mn=nm”类比得到“a·b=b·a”;
②“(m+n)t=mt+nt”类比得到“(a+b)·c=a·c+b·c”;
③“t≠0,mt=ntm=n”类比得到“c≠0,a·c=b·ca=b”;
④“|m·n|=|m|·|n|”类比得到“|a·b|=|a|·|b|”;
⑤“(m·n)t=m(n·t)”类比得到“(a·b)·c=a(b·c)”;
⑥“![]() ”类比得到
”类比得到![]() .以上的式子中,类比得到的结论正确的是________.
.以上的式子中,类比得到的结论正确的是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如下部分频率分布直方图.观察图形给出的信息,回答下列问题:

(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)从成绩是[40,50)和[90,100]的学生中选两人,求他们在同一分数段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知AB为半圆O的直径,AB=4,C为半圆上一点,过点C作半圆的切线CD,过点A作AD⊥CD于D,交半圆于点E,DE=1.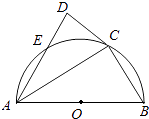
(1)求证:AC平分∠BAD;
(2)求BC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线y2=2px(p>0)与直线y=x+1相切,A(x1,y1),B(x2,y2)(x1≠x2)是抛物线上两个动点,F为抛物线的焦点,且|AF|+|BF|=8.
(1)求p的值.
(2)线段AB的垂直平分线l与x轴的交点是否为定点?若是,求出交点坐标;若不是,说明理由.
(3)求直线l的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x3+ax2+bx+1的导数![]() 满足
满足![]() ,其中常数a,b∈R.
,其中常数a,b∈R.
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)设![]() ,求函数g(x)的极值.
,求函数g(x)的极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 ![]() ,
, ![]() 为非零向量,则“存在负数λ,使得
为非零向量,则“存在负数λ,使得 ![]() =λ
=λ ![]() ”是
”是 ![]()
![]() <0”的( )
<0”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com