【题目】在平面直角坐标系xOy中，已知椭圆C：
的离心率
，F1，F2分别为左、右焦点，过F1的直线交椭圆C于P，Q两点，且
的周长为8.
（1）求椭圆c的方程；
（2）设过点M(3,0)的直线交椭圆C于不同两点A，B，N为椭圆上一点，且满足
（O为坐标原点），当
时，求实数t的取值范围.
【答案】（1）
；（2）
【解析】
（1）利用已知条件，求出a，b，即可得到椭圆方程;（2）设A（x1，y1），B（x2，y2），N（x，y），AB的方程为y=k（x﹣3），联立直线和椭圆，整理得（1+4k2）x2﹣24k2x+36k2﹣4=0．利用判别式以及韦达定理，结合
=t（x，y），求出N的坐标，代入椭圆方程，利用弦长公式，化简不等式，求出K的范围，然后求解t的范围．
（1）∵
，∴
.
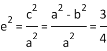又∵
，∴
，∴
，∴椭圆
的方程是
.
（2）设
，
，
，
的方程为
，
由
，整理得
.
由
，得
.
∵
，
，
∴
，
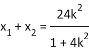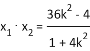则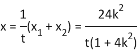
，
.
由点
在椭圆上，得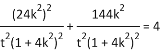
，化简得
. ①
又由
，即
，
将
，
代入得
，
化简，得
，则
，
，∴
. ②
由①，得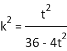
，联立②，解得
.
∴
或
，即
.
名校课堂系列答案科目：高中数学 来源： 题型：
【题目】某公司计划购买2台机器，该种机器使用三年后即被淘汰．机器有一易损零件，在购进机器时，可以额外购买这种零件作为备件，每个200元．在机器使用期间，如果备件不足再购买，则每个500元．现需决策在购买机器时应同时购买几个易损零件，为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数，得下面柱状图：
以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率，记X表示2台机器三年内共需更换的易损零件数，n表示购买2台机器的同时购买的易损零件数．
(1)求X的分布列；
(2)若要求P(X≤n)≤0.5，确定n的最小值；
(3)以购买易损零件所需费用的期望值为决策依据，在n＝19与n＝20之中选其一，应选用哪个？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某中学团委组织了“弘扬奥运精神，爱我中华”的知识竞赛，从参加考试的学生中抽出60名学生，将其成绩(均为整数)分成六段[40,50)，[50,60)，…，[90,100]后画出如下部分频率分布直方图．观察图形给出的信息，回答下列问题：
(1)求第四小组的频率，并补全这个频率分布直方图；
(2)估计这次考试的及格率(60分及以上为及格)和平均分；
(3)从成绩是[40,50)和[90,100]的学生中选两人，求他们在同一分数段的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】抛物线y2=2px(p>0)与直线y=x+1相切,A(x1,y1),B(x2,y2)(x1≠x2)是抛物线上两个动点,F为抛物线的焦点,且|AF|+|BF|=8.
(1)求p的值.
(2)线段AB的垂直平分线l与x轴的交点是否为定点?若是,求出交点坐标;若不是,说明理由.
(3)求直线l的斜率的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数f（x）＝x3＋ax2＋bx＋1的导数
满足
，其中常数a，b∈R.
（1）求曲线y＝f（x）在点（1，f（1））处的切线方程；
（2）设
，求函数g（x）的极值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
=1(a>b>0)的左、右焦点分别为F1,F2,短轴两个端点为A,B,且四边形F1AF2B是边长为2的正方形.
(1)求椭圆的方程;
(2)若C,D分别是椭圆的左、右端点,动点M满足MD⊥CD,连接CM,交椭圆于点P.证明:
为定值.
(3)在(2)的条件下,试问x轴上是否存在异于点C的定点Q,使得以MP为直径的圆恒过直线DP,MQ的交点?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）= 
，设a∈R，若关于x的不等式f（x）≥| 
+a|在R上恒成立，则a的取值范围是（ ）
A.[﹣ 
，2]
B.[﹣ ， 
]
C.[﹣2 
，2]
D.[﹣2 ， ]
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=excosx﹣x．（13分）
（1）求曲线y=f（x）在点（0，f（0））处的切线方程；
（2）求函数f（x）在区间[0， 
]上的最大值和最小值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
