
【题目】已知函数f(x)=  ,设a∈R,若关于x的不等式f(x)≥|
,设a∈R,若关于x的不等式f(x)≥| ![]() +a|在R上恒成立,则a的取值范围是( )
+a|在R上恒成立,则a的取值范围是( )
A.[﹣ ![]() ,2]
,2]
B.[﹣ ![]() ,
, ![]() ]
]
C.[﹣2 ![]() ,2]
,2]
D.[﹣2 ![]() ,
, ![]() ]
]
【答案】A
【解析】解:当x≤1时,关于x的不等式f(x)≥| ![]() +a|在R上恒成立,
+a|在R上恒成立,
即为﹣x2+x﹣3≤ ![]() +a≤x2﹣x+3,
+a≤x2﹣x+3,
即有﹣x2+ ![]() x﹣3≤a≤x2﹣
x﹣3≤a≤x2﹣ ![]() x+3,
x+3,
由y=﹣x2+ ![]() x﹣3的对称轴为x=
x﹣3的对称轴为x= ![]() <1,可得x=
<1,可得x= ![]() 处取得最大值﹣
处取得最大值﹣ ![]() ;
;
由y=x2﹣ ![]() x+3的对称轴为x=
x+3的对称轴为x= ![]() <1,可得x=
<1,可得x= ![]() 处取得最小值
处取得最小值 ![]() ,
,
则﹣ ![]() ≤a≤
≤a≤ ![]() ①
①
当x>1时,关于x的不等式f(x)≥| ![]() +a|在R上恒成立,
+a|在R上恒成立,
即为﹣(x+ ![]() )≤
)≤ ![]() +a≤x+
+a≤x+ ![]() ,
,
即有﹣( ![]() x+
x+ ![]() )≤a≤
)≤a≤ ![]() +
+ ![]() ,
,
由y=﹣( ![]() x+
x+ ![]() )≤﹣2
)≤﹣2 ![]() =﹣2
=﹣2 ![]() (当且仅当x=
(当且仅当x= ![]() >1)取得最大值﹣2
>1)取得最大值﹣2 ![]() ;
;
由y= ![]() x+
x+ ![]() ≥2
≥2 ![]() =2(当且仅当x=2>1)取得最小值2.
=2(当且仅当x=2>1)取得最小值2.
则﹣2 ![]() ≤a≤2②
≤a≤2②
由①②可得,﹣ ![]() ≤a≤2.
≤a≤2.
故选:A.


科目:高中数学 来源: 题型:
【题目】已知椭圆C与椭圆E: ![]() 共焦点,并且经过点
共焦点,并且经过点 ![]() ,
,
(1)求椭圆C的标准方程;
(2)在椭圆C上任取两点P、Q,设PQ所在直线与x轴交于点M(m,0),点P1为点P关于轴x的对称点,QP1所在直线与x轴交于点N(n,0),探求mn是否为定值?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知椭圆C:![]() 的离心率
的离心率![]() ,F1,F2分别为左、右焦点,过F1的直线交椭圆C于P,Q两点,且
,F1,F2分别为左、右焦点,过F1的直线交椭圆C于P,Q两点,且![]() 的周长为8.
的周长为8.
(1)求椭圆c的方程;
(2)设过点M(3,0)的直线交椭圆C于不同两点A,B,N为椭圆上一点,且满足![]() (O为坐标原点),当
(O为坐标原点),当![]() 时,求实数t的取值范围.
时,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,动圆经过点M(a﹣2,0),N(a+2,0),P(0,﹣2),其中a∈R.
(1)求动圆圆心的轨迹E的方程;
(2)过点P作直线l交轨迹E于不同的两点A、B,直线OA与直线OB分别交直线y=2于两点C、D,记△ACD与△BCD的面积分别为S1 , S2 . 求S1+S2的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆![]() 的圆心在
的圆心在![]() 轴上,并且过
轴上,并且过![]() 两点.
两点.
(1)求圆![]() 的方程;
的方程;
(2)设直线![]() 与圆
与圆![]() 交于
交于![]() 两点,那么以
两点,那么以![]() 为直径的圆能否经过原点,若能,请求出直线
为直径的圆能否经过原点,若能,请求出直线![]() 的方程;若不能,请说明理由.
的方程;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲地到乙地要经过3个十字路口,设各路口信号灯工作相互独立,且在各路口遇到红灯的概率分别为 ![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)设X表示一辆车从甲地到乙地遇到红灯的个数,求随机变量X的分布列和数学期望;
(Ⅱ)若有2辆车独立地从甲地到乙地,求这2辆车共遇到1个红灯的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正四棱台ABCD-A1B1C1D1中,上底面A1B1C1D1边长为1,下底面ABCD边长为2,侧棱与底面所成的角为60°,则异面直线AD1与B1C所成角的余弦值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
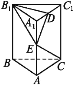
【题目】如图,在直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰三角形,AC=2a,BB1=3a,D是A1C1的中点,点E在棱AA1上,要使CE⊥平面B1DE,则AE=_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{xn}满足:x1=1,xn=xn+1+ln(1+xn+1)(n∈N*),证明:当n∈N*时,
(Ⅰ)0<xn+1<xn;
(Ⅱ)2xn+1﹣xn≤ ![]() ;
;
(Ⅲ) ![]() ≤xn≤
≤xn≤ ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com