
分析 (1)由曲线C1的参数方程能求出曲线C1的直角坐标方程,从而能求出曲线C1的极坐标方程.由曲线C2的参数方程能求出曲线C2的直角坐标方程,从而能求出曲线C2的极坐标方程.
(2)设点P的极坐标为P(ρ1,α),即ρ1=2cosα,设点Q的坐标为Q(${ρ}_{2},α-\frac{π}{6}$),即${ρ}_{2}=2sin(α-\frac{π}{6})$,mh|OP|•|OQ|=ρ1•ρ2=2cos$α•2sin(α-\frac{π}{6})$=2sin(2$α-\frac{π}{6}$)-1,能求出|OP|•|OQ|的最大值.
解答 解:(1)∵曲线C1的参数方程为$\left\{\begin{array}{l}{x=1+cosα}\\{y=sinα}\end{array}\right.$(α为参数),
∴曲线C1的直角坐标方程为(x-1)2+y2=1,
即x2+y2-2x=0,
∴曲线C1的极坐标方程为ρ2-2ρcosθ=0,即ρ=2cosθ.
∵曲线C2的参数方程为$\left\{\begin{array}{l}{x=cosβ}\\{y=1+sinβ}\end{array}\right.$(β为参数),
∴曲线C2的普通方程x2+(y-1)2=1,即x2+y2-2y=0,
∴曲线C2的极坐标方程为ρ2-2ρsinθ=0,即ρ=2sinθ.
(2)设点P的极坐标为P(ρ1,α),即ρ1=2cosα,
设点Q的坐标为Q(${ρ}_{2},α-\frac{π}{6}$),即${ρ}_{2}=2sin(α-\frac{π}{6})$,
∴|OP|•|OQ|=ρ1•ρ2=2cos$α•2sin(α-\frac{π}{6})$=4cosα($\frac{\sqrt{3}}{2}$sin$α-\frac{1}{2}cosα$)
=2$\sqrt{3}$sinαcosα-2cos2α=$\sqrt{3}sin2α$-cos2α-1=2sin(2$α-\frac{π}{6}$)-1,
∵α∈($\frac{π}{6},\frac{π}{2}$),∴$2α-\frac{π}{6}$∈($\frac{π}{6},\frac{5π}{6}$),
当2$α-\frac{π}{6}$=$\frac{π}{2}$,即$α=\frac{π}{3}$时,|OP|•|OQ|取最大值1.
点评 本题考查曲线的极坐标方程的求法,考查两线段积的最大值的求法,考查极坐标方程、直角坐标方程、参数方程的互化等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
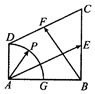 在直角梯形ABCD中,AB⊥AD,AD∥BC,AB=BC=2AD=2,E,F分别为BC,CD的中点,以A为圆心,AD为半径的圆交AB于G,点P在$\widehat{DG}$上运动(如图).若$\overrightarrow{AP}$=λ$\overrightarrow{AE}$+μ$\overrightarrow{BF}$,其中λ,μ∈R,则6λ+μ的取值范围是( )
在直角梯形ABCD中,AB⊥AD,AD∥BC,AB=BC=2AD=2,E,F分别为BC,CD的中点,以A为圆心,AD为半径的圆交AB于G,点P在$\widehat{DG}$上运动(如图).若$\overrightarrow{AP}$=λ$\overrightarrow{AE}$+μ$\overrightarrow{BF}$,其中λ,μ∈R,则6λ+μ的取值范围是( )| A. | [1,$\sqrt{2}$] | B. | [$\sqrt{2}$,2$\sqrt{2}$] | C. | [2,2$\sqrt{2}$] | D. | [1,2$\sqrt{2}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com