
【题目】某服装加工厂为了提高市场竞争力,对其中一台生产设备提出了甲、乙两个改进方案:甲方案是引进一台新的生产设备,需一次性投资1000万元,年生产能力为30万件;乙方案是将原来的设备进行升级改造,需一次性投入700万元,年生产能力为20万件.根据市场调查与预测,该产品的年销售量的频率分布直方图如图所示,无论是引进新生产设备还是改造原有的生产设备,设备的使用年限均为6年,该产品的销售利润为15元/件(不含一次性设备改进投资费用).
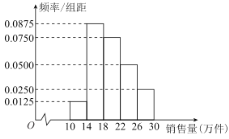
(1)根据年销售量的频率分布直方图,估算年销量的平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)将年销售量落入各组的频率视为概率,各组的年销售量用该组区间的中点值作年销量的估计值,并假设每年的销售量相互独立.
①根据频率分布直方图估计年销售利润不低于270万元的概率:
②若以该生产设备6年的净利润的期望值作为决策的依据,试判断该服装厂应选择哪个方案.(6年的净利润=6年销售利润-设备改进投资费用)
【答案】(1)19.8万件(2)①0.6 ②乙方案.
【解析】
(1)利用小矩形的中点乘以小矩形的面积之和,从而求得平均数;
(2)①由题意得只有当年销售量不低于18万件时年销售利润才不低于270万,再从频率分布直方图中,估计年销售利润不低于270万的概率;
②分别计算两种方案6年的净利润的期望值,再比较大小,从而得到结论。
(1)年销量的平均数![]() (万件).
(万件).
(2)①该产品的销售利润为15元/件,
由题意得只有当年销售量不低于18万件时年销售利润才不低于270万,
所以年销售利润不低于270万的概率![]() .
.
②设甲方案的年销售量为X万件,由(1)可知甲方案的年销售量的期望![]() ,
,
所以甲方案6年的净利润的期望值为![]() (万元).
(万元).
设乙方案的年销售量为Y万件,则乙方案的年销售量的分布列为
Y | 12 | 16 | 20 |
P | 0.05 | 0.35 | 0.6 |
所以乙方案的年销售量期望![]() (万件),
(万件),
所以乙方案6年的净利润的期望值为![]() (万元),
(万元),
因为乙方案的净利润的期望值大于甲方案的净利润的期望值,
所以企业应该选择乙方案.


 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】某省高考改革方案指出:该省高考考生总成绩将由语文数学英语3门统一高考成绩和学生从思想政治、历史、地理、物理、化学、生物6门等级性考试科目中自主选择3个,按获得该次考试有效成绩的考生(缺考考生或未得分的考生除外)总人数的相应比例的基础上划分等级,位次由高到低分为A、B、C、D、E五等21级,该省的某市为了解本市![]() 万名学生的某次选考化学成绩水平,统计在全市范围内选考化学的原始成绩,发现其成绩服从正态分布
万名学生的某次选考化学成绩水平,统计在全市范围内选考化学的原始成绩,发现其成绩服从正态分布![]()
![]() ,现从某校随机抽取了
,现从某校随机抽取了![]() 名学生,将所得成绩整理后,绘制出如图所示的频率分布直方图.
名学生,将所得成绩整理后,绘制出如图所示的频率分布直方图.

(1)估算该校![]() 名学生成绩的平均值
名学生成绩的平均值![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)现从该校![]() 名考生成绩在
名考生成绩在![]() 的学生中随机抽取两人,该两人成绩排名(从高到低)在全市前
的学生中随机抽取两人,该两人成绩排名(从高到低)在全市前![]() 名的人数记为
名的人数记为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.参考数据:若
的分布列和数学期望.参考数据:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() 3,g(x)=alnx﹣2x(a∈R).
3,g(x)=alnx﹣2x(a∈R).
(1)讨论g(x)的单调性;
(2)是否存在实数a,使不等式f(x)≥g(x)恒成立?如果存在,求出a的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明和父母都喜爱《中国好声音》这栏节目,![]() 年
年![]() 月
月![]() 日晚在鸟巢进行中国好声音终极决赛,四强选手分别为李荣浩战队的邢晗铭,那英战队的斯丹曼簇,王力宏战队的李芷婷,庾澄庆战队的陈其楠,决赛后四位选手相应的名次为
日晚在鸟巢进行中国好声音终极决赛,四强选手分别为李荣浩战队的邢晗铭,那英战队的斯丹曼簇,王力宏战队的李芷婷,庾澄庆战队的陈其楠,决赛后四位选手相应的名次为![]() 、
、![]() 、
、![]() 、
、![]() ,某网站为提升娱乐性,邀请网友在比赛结束前对选手名次进行预测.现用
,某网站为提升娱乐性,邀请网友在比赛结束前对选手名次进行预测.现用![]() 、
、![]() 、
、![]() 、
、![]() 表示某网友对实际名次为
表示某网友对实际名次为![]() 、
、![]() 、
、![]() 、
、![]() 的四位选手名次做出的一种等可能的预测排列,
的四位选手名次做出的一种等可能的预测排列,![]() 是该网友预测的名次与真实名次的偏离程度的一种描述.
是该网友预测的名次与真实名次的偏离程度的一种描述.
(1)求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)按(1)中的结果,若小明家三人的排序号与真实名次的偏离程度都是![]() ,计算出现这种情况的概率(假定小明家每个人排序相互独立).
,计算出现这种情况的概率(假定小明家每个人排序相互独立).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C的对边分别为a,b,c,且asinB=bsin(A+![]() ).
).
(1)求A;
(2)若b,![]() a,c成等差数列,△ABC的面积为2
a,c成等差数列,△ABC的面积为2![]() ,求a.
,求a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四面体ABCD中,AC=6,BA=BC=5,AD=CD=3![]() .
.
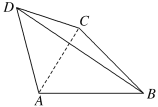
(1)求证:AC⊥BD;
(2)当四面体ABCD的体积最大时,求点A到平面BCD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ).其中常数
).其中常数![]() 是自然对数的底数.
是自然对数的底数.
(1)若![]() ,求
,求![]() 在
在![]() 上的极大值点;
上的极大值点;
(2)(i)证明![]() 在
在 上单调递增;
上单调递增;
(ii)求关于x的方程![]() 在
在![]() 上的实数解的个数.
上的实数解的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥S-ABC中,侧棱SA,SB,SC两两成等角,且长度分别为a,b,c,设二面角S-BC-A,S-AC–B,S-AB-C的大小为![]() ,若
,若![]() 则α,β,γ的大小关系是( )
则α,β,γ的大小关系是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com