【题目】已知△ABC的内角A，B，C的对边分别为a，b，c，且asinB=bsin（A+
）．
（1）求A；
（2）若b，
a，c成等差数列，△ABC的面积为2
，求a．
【答案】（1）
； （2）
.
【解析】
（1）由正弦定理化简已知可得sinA=sin（A+），结合范围A∈（0，π），即可计算求解A的值；
（2）利用等差数列的性质可得b+c=
，利用三角形面积公式可求bc的值，进而根据余弦定理即可解得a的值．
（1）∵asinB=bsin（A+）．
∴由正弦定理可得：sinAsinB=sinBsin（A+）．
∵sinB≠0，
∴sinA=sin（A+）．
∵A∈（0，π），可得：A+A+=π，
∴A=．
（2）∵b，
a，c成等差数列，
∴b+c=，
∵△ABC的面积为2
，可得：S△ABC=
bcsinA=2，
∴
=2，解得bc=8，
∴由余弦定理可得：a2=b2+c2﹣2bccosA=（b+c）2﹣2bc﹣2bccos
=（b+c）2﹣3bc=（a）2﹣24，
∴解得：a=2．
培优好卷单元加期末卷系列答案
一线名师权威作业本系列答案科目：高中数学 来源： 题型：
【题目】△ABC的内角A，B，C的对边分别为
，已知
且
．
(1)求角
；
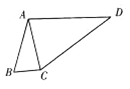
(2)如图，D为△ABC外一点，若在平面四边形ABCD中，
，求△ACD面积的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
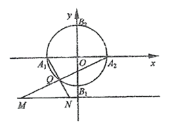
【题目】在平面直角坐标系xOy中，圆O：
与坐标轴分别交于A1，A2，B1，B2(如图)．
（1）点Q是圆O上除A1，A2外的任意点(如图1)，直线A1Q，A2Q与直线
交于不同的两点M，N，求线段MN长的最小值；
（2）点P是圆O上除A1，A2，B1，B2外的任意点(如图2)，直线B2P交x轴于点F，直线A1B2交A2P于点E．设A2P的斜率为k，EF的斜率为m，求证：2m﹣k为定值．
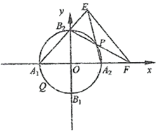
（图1） （图2）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】定义：如果数列
的任意连续三项均能构成一个三角形的三边长，则称为三角形”数列对于“三角形”数列，如果函数
使得
仍为一个三角形”数列，则称是数列的“保三角形函数”
．
（1）已知是首项为2，公差为1的等差数列，若
，
是数列的保三角形函数”，求
的取值范围；
（2）已知数列
的首项为2019，
是数列的前
项和，且满足
，证明是“三角形”数列；
（3）求证：函数
，
是数列1，
，
的“保三角形函数”的充要条件是
，
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】现对一块边长8米的正方形场地ABCD进行改造，点E为线段BC的中点，点F在线段CD或AD上（异于A，C），设
（米），
的面积记为
（平方米），其余部分面积记为
（平方米）.
（1）当
（米）时，求
的值；
（2）求函数的最大值；
（3）该场地中部分改造费用为
（万元），其余部分改造费用为
（万元），记总的改造费用为W（万元），求W取最小值时x的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公司的电子新产品未上市时，原定每件售价100元，经过市场调研发现，该电子新产品市场潜力很大，该公司决定从第一周开始销售时，该电子产品每件售价比原定售价每周涨价4元，5周后开始保持120元的价格平稳销售，10周后由于市场竞争日益激烈，每周降价2元，直到15周结束，该产品不再销售.
（Ⅰ）求售价
（单位：元）与周次
（
）之间的函数关系式；
（Ⅱ）若此电子产品的单件成本
（单位：元）与周次
之间的关系式为
，
，，试问：此电子产品第几周的单件销售利润（销售利润
售价
成本）最大？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
