
【题目】定义:如果数列![]() 的任意连续三项均能构成一个三角形的三边长,则称
的任意连续三项均能构成一个三角形的三边长,则称![]() 为三角形”数列对于“三角形”数列
为三角形”数列对于“三角形”数列![]() ,如果函数
,如果函数![]() 使得
使得![]() 仍为一个三角形”数列,则称
仍为一个三角形”数列,则称![]() 是数列
是数列![]() 的“保三角形函数”
的“保三角形函数”![]() .
.
(1)已知![]() 是首项为2,公差为1的等差数列,若
是首项为2,公差为1的等差数列,若![]() ,
,![]() 是数列
是数列![]() 的保三角形函数”,求
的保三角形函数”,求![]() 的取值范围;
的取值范围;
(2)已知数列![]() 的首项为2019,
的首项为2019,![]() 是数列
是数列![]() 的前
的前![]() 项和,且满足
项和,且满足![]() ,证明
,证明![]() 是“三角形”数列;
是“三角形”数列;
(3)求证:函数![]() ,
,![]() 是数列1,
是数列1,![]() ,
,![]() 的“保三角形函数”的充要条件是
的“保三角形函数”的充要条件是![]() ,
,![]() .
.
【答案】(1)![]() ;(2)见解析;(3)见解析.
;(2)见解析;(3)见解析.
【解析】
(1)先由条件得![]() 是三角形数列,再利用
是三角形数列,再利用![]() ,
,![]() 是数列
是数列![]() 的“保三角形函数”,得到
的“保三角形函数”,得到![]() ,解得
,解得![]() 的取值范围;
的取值范围;
(2)先利用条件求出数列![]() 的通项公式,再证明其满足“三角形”数列的定义即可;
的通项公式,再证明其满足“三角形”数列的定义即可;
(3)根据函数![]() ,
,![]() ,
,![]() 是数列1,
是数列1,![]() ,
,![]() 的“保三角形函数”,可以得到①1,
的“保三角形函数”,可以得到①1,![]() ,
,![]() 是三角形数列,所以
是三角形数列,所以![]() ,即
,即![]() ,②数列中的各项必须在定义域内,即
,②数列中的各项必须在定义域内,即![]() ,③
,③![]() ,
,![]() ,
,![]() 是三角形数列;结论为在利用
是三角形数列;结论为在利用![]() ,
,![]() 是单调递减函数,就可求出对应
是单调递减函数,就可求出对应![]() 的范围,即可证明.
的范围,即可证明.
(1)解:显然![]() ,
,![]() 对任意正整数都成立,即
对任意正整数都成立,即![]() 是三角形数列,
是三角形数列,
因为![]() ,显然有
,显然有![]() ,
,
由![]() 得
得![]() ,解得
,解得![]() ,
,
所以当![]() 时,
时,![]() 是数列
是数列![]() 的“保三角形函数”;
的“保三角形函数”;
(2)证:由![]() ,
,
当![]() 时,
时,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
当![]() 时,即
时,即![]() ,解得
,解得![]() ,∴
,∴![]() ,
,
∴数列![]() 是以2019为首项,以
是以2019为首项,以![]() 为公比的等比数列,
为公比的等比数列,
∴![]() ,
,
显然![]() ,因为
,因为![]()
![]()
![]() ,
,
所以![]() 是“三角形”数列;
是“三角形”数列;
(3)证:函数![]() ,
,![]() 是数列1,
是数列1,![]() ,
,![]() 的“保三角形函数”,必须满足三个条件:
的“保三角形函数”,必须满足三个条件:
①1,![]() ,
,![]() 是三角形数列,所以
是三角形数列,所以![]() ,即
,即![]() ;
;
②数列中的各项必须在定义域内,即![]() ;
;
③![]() ,
,![]() ,
,![]() 是三角形数列,
是三角形数列,
由于![]() ,
,![]() 是单调递减函数,所以
是单调递减函数,所以![]() ,解得
,解得![]() ,
,
所以函数![]() ,
,![]() 是数列1,
是数列1,![]() ,
,![]() 的“保三角形函数”的充要条件是
的“保三角形函数”的充要条件是![]() ,
,![]() .
.


 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC—A1B1C1中,CA=CB=4,![]() ,E,F分别为AC,CC1的中点,则直线EF与平面AA1B1B所成的角是
,E,F分别为AC,CC1的中点,则直线EF与平面AA1B1B所成的角是
A. 30° B. 45° C. 60° D. 90°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数,
为常数,![]() 且
且![]() ),且数列
),且数列![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列.
的等差数列.
(1)求证:数列![]() 是等比数列;
是等比数列;
(2)若![]() ,当
,当![]() 时,求数列
时,求数列![]() 的前
的前![]() 项和
项和![]() 的最小值;
的最小值;
(3)若![]() ,问是否存在实数
,问是否存在实数![]() ,使得
,使得![]() 是递增数列?若存在,求出
是递增数列?若存在,求出![]() 的范围;若不存在,说明理由.
的范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数x,y满足x3<y3,则下列不等式中恒成立的是( )
A. (![]() )x>(
)x>(![]() )y B. ln(x2+1)>ln(y2+1)
)y B. ln(x2+1)>ln(y2+1)
C. ![]() D. tanx>tany
D. tanx>tany
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校兴趣小组在如图所示的矩形区域![]() 内举行机器人拦截挑战赛,在
内举行机器人拦截挑战赛,在![]() 处按
处按![]() 方向释放机器人甲,同时在
方向释放机器人甲,同时在![]() 处按某方向释放机器人乙,设机器人乙在
处按某方向释放机器人乙,设机器人乙在![]() 处成功拦截机器人甲,若点
处成功拦截机器人甲,若点![]() 在矩形区城
在矩形区城![]() 内(包含边界),则挑战成功,否则挑战失败,已知
内(包含边界),则挑战成功,否则挑战失败,已知![]() 米,
米,![]() 为
为![]() 中点,机器人乙的速度是机器人甲的速度的2倍,比赛中两机器人均按匀速直线远动方式行进.
中点,机器人乙的速度是机器人甲的速度的2倍,比赛中两机器人均按匀速直线远动方式行进.
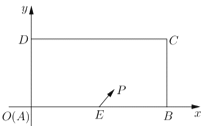
(1)如图建系,求![]() 的轨迹方程;
的轨迹方程;
(2)记![]() 与
与![]() 的夹角为
的夹角为![]() ,
,![]() ,如何设计
,如何设计![]() 的长度,才能确保无论
的长度,才能确保无论![]() 的值为多少,总可以通过设置机器人乙的释放角度使之挑战成功?
的值为多少,总可以通过设置机器人乙的释放角度使之挑战成功?
(3)若![]() 与
与![]() 的夹角为
的夹角为![]() ,
,![]() 足够长,则如何设置机器人乙的释放角度,才能挑战成功?
足够长,则如何设置机器人乙的释放角度,才能挑战成功?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C的对边分别为a,b,c,且asinB=bsin(A+![]() ).
).
(1)求A;
(2)若b,![]() a,c成等差数列,△ABC的面积为2
a,c成等差数列,△ABC的面积为2![]() ,求a.
,求a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在测量一根新弹簧的劲度系数时,测得了如下的结果:
所挂重量( | 1 | 2 | 3 | 5 | 7 | 9 |
弹簧长度( | 11 | 12 | 12 | 13 | 14 | 16 |
(1)请在下图坐标系中画出上表所给数据的散点图;

(2)若弹簧长度与所挂物体重量之间的关系具有线性相关性,请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(3)根据回归方程,求挂重量为![]() 的物体时弹簧的长度.所求得的长度是弹簧的实际长度吗?为什么?
的物体时弹簧的长度.所求得的长度是弹簧的实际长度吗?为什么?
注:本题中的计算结果保留小数点后两位.
(参考公式: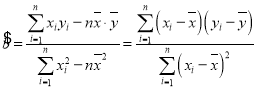 ,
,![]() )
)
(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com