
【题目】设棱锥M-ABCD的底面是正方形,且MA=MD,MA⊥AB.如果△AMD的面积为1,试求能够放入这个棱锥的最大球的半径.
【答案】![]()
【解析】
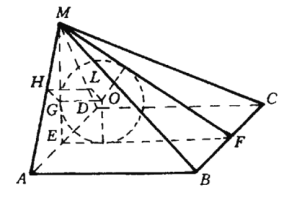
如图,因为AB⊥AD,AB⊥MA,所以,AB垂直于平面MAD,
由此知平面MAD垂直平面AC.
设E是AD的中点,F是BC的中点,则ME⊥AD,所以,ME垂直平面AC,ME⊥EF.
设球O是与平面MAD,AC,MBC都相切的球.
不失一般性,可设O在平面MEF上.于是O为△MEF的内心.
设球O的半径为r,则![]() .
.
设AD=EF=a,因为![]() ,所以
,所以![]() ,
,
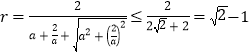 ,
,
且当![]() ,即
,即![]() 时,上式取等号,所以,当AD=ME=
时,上式取等号,所以,当AD=ME=![]() 时,
时,
与三个面MAD,AC,MBC都相切的球的半径最大,并且这个最大半径为![]() .
.
作OG⊥ME于G,易证OG//平面MAB,G到平面MAB的距离就是O到平面MAB的距离.
过G作MH⊥MA于H,则GH是G到平面MAB的距离.
![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,
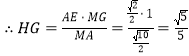 .
.
![]() ,
,
故O到平面MAB的距离大于球O的半径r,同样O到面MCD的距离也大于球O的半径r,
故球O在棱锥M-ABCD内,并且不可能再大.
据此可得所求的最大球的半径为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知曲线M:![]() 的左、右顶点分别为A,B,设P是曲线M上的任意一点.
的左、右顶点分别为A,B,设P是曲线M上的任意一点.
(1)当P异于A,B时,记直线PA、PB的斜率分别为![]() 、
、![]() 则
则![]() 是否为定值,请说明理由.
是否为定值,请说明理由.
(2)已知点C在曲线M长轴上(异于A、B两点),且![]() 的最大值为7,求点C的坐标.
的最大值为7,求点C的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:如果数列![]() 的任意连续三项均能构成一个三角形的三边长,则称
的任意连续三项均能构成一个三角形的三边长,则称![]() 为三角形”数列对于“三角形”数列
为三角形”数列对于“三角形”数列![]() ,如果函数
,如果函数![]() 使得
使得![]() 仍为一个三角形”数列,则称
仍为一个三角形”数列,则称![]() 是数列
是数列![]() 的“保三角形函数”
的“保三角形函数”![]() .
.
(1)已知![]() 是首项为2,公差为1的等差数列,若
是首项为2,公差为1的等差数列,若![]() ,
,![]() 是数列
是数列![]() 的保三角形函数”,求
的保三角形函数”,求![]() 的取值范围;
的取值范围;
(2)已知数列![]() 的首项为2019,
的首项为2019,![]() 是数列
是数列![]() 的前
的前![]() 项和,且满足
项和,且满足![]() ,证明
,证明![]() 是“三角形”数列;
是“三角形”数列;
(3)求证:函数![]() ,
,![]() 是数列1,
是数列1,![]() ,
,![]() 的“保三角形函数”的充要条件是
的“保三角形函数”的充要条件是![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现对一块边长8米的正方形场地ABCD进行改造,点E为线段BC的中点,点F在线段CD或AD上(异于A,C),设![]() (米),
(米),![]() 的面积记为
的面积记为![]() (平方米),其余部分面积记为
(平方米),其余部分面积记为![]() (平方米).
(平方米).
(1)当![]() (米)时,求
(米)时,求![]() 的值;
的值;
(2)求函数![]() 的最大值;
的最大值;
(3)该场地中![]() 部分改造费用为
部分改造费用为![]() (万元),其余部分改造费用为
(万元),其余部分改造费用为![]() (万元),记总的改造费用为W(万元),求W取最小值时x的值.
(万元),记总的改造费用为W(万元),求W取最小值时x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,边长为4的正方形![]() 中,半径为1的动圆Q的圆心Q在边CD和DA上移动(包含端点A,C,D),P是圆Q上及其内部的动点,设,
中,半径为1的动圆Q的圆心Q在边CD和DA上移动(包含端点A,C,D),P是圆Q上及其内部的动点,设,![]() 则
则![]() 的取值范围是_____________.
的取值范围是_____________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).M是曲线
为参数).M是曲线![]() 上的动点,将线段OM绕O点顺时针旋转
上的动点,将线段OM绕O点顺时针旋转![]() 得到线段ON,设点N的轨迹为曲线
得到线段ON,设点N的轨迹为曲线![]() .以坐标原点O为极点,
.以坐标原点O为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在(1)的条件下,若射线![]() 与曲线
与曲线![]() 分别交于A, B两点(除极点外),且有定点
分别交于A, B两点(除极点外),且有定点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com