
【题目】现对一块边长8米的正方形场地ABCD进行改造,点E为线段BC的中点,点F在线段CD或AD上(异于A,C),设![]() (米),
(米),![]() 的面积记为
的面积记为![]() (平方米),其余部分面积记为
(平方米),其余部分面积记为![]() (平方米).
(平方米).
(1)当![]() (米)时,求
(米)时,求![]() 的值;
的值;
(2)求函数![]() 的最大值;
的最大值;
(3)该场地中![]() 部分改造费用为
部分改造费用为![]() (万元),其余部分改造费用为
(万元),其余部分改造费用为![]() (万元),记总的改造费用为W(万元),求W取最小值时x的值.
(万元),记总的改造费用为W(万元),求W取最小值时x的值.
科目:高中数学 来源: 题型:
【题目】已知两个定点![]() ,
,![]() , 动点
, 动点![]() 满足
满足![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() :
:![]() .
.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)若![]() 与曲线
与曲线![]() 交于不同的
交于不同的![]() 、
、![]() 两点,且
两点,且![]() (
(![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的斜率;
的斜率;
(3)若![]() ,
,![]() 是直线
是直线![]() 上的动点,过
上的动点,过![]() 作曲线
作曲线![]() 的两条切线
的两条切线![]() 、
、![]() ,切点为
,切点为![]() 、
、![]() ,探究:直线
,探究:直线![]() 是否过定点,若存在定点请写出坐标,若不存在则说明理由.
是否过定点,若存在定点请写出坐标,若不存在则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数,
为常数,![]() 且
且![]() ),且数列
),且数列![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列.
的等差数列.
(1)求证:数列![]() 是等比数列;
是等比数列;
(2)若![]() ,当
,当![]() 时,求数列
时,求数列![]() 的前
的前![]() 项和
项和![]() 的最小值;
的最小值;
(3)若![]() ,问是否存在实数
,问是否存在实数![]() ,使得
,使得![]() 是递增数列?若存在,求出
是递增数列?若存在,求出![]() 的范围;若不存在,说明理由.
的范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校兴趣小组在如图所示的矩形区域![]() 内举行机器人拦截挑战赛,在
内举行机器人拦截挑战赛,在![]() 处按
处按![]() 方向释放机器人甲,同时在
方向释放机器人甲,同时在![]() 处按某方向释放机器人乙,设机器人乙在
处按某方向释放机器人乙,设机器人乙在![]() 处成功拦截机器人甲,若点
处成功拦截机器人甲,若点![]() 在矩形区城
在矩形区城![]() 内(包含边界),则挑战成功,否则挑战失败,已知
内(包含边界),则挑战成功,否则挑战失败,已知![]() 米,
米,![]() 为
为![]() 中点,机器人乙的速度是机器人甲的速度的2倍,比赛中两机器人均按匀速直线远动方式行进.
中点,机器人乙的速度是机器人甲的速度的2倍,比赛中两机器人均按匀速直线远动方式行进.
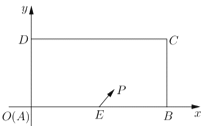
(1)如图建系,求![]() 的轨迹方程;
的轨迹方程;
(2)记![]() 与
与![]() 的夹角为
的夹角为![]() ,
,![]() ,如何设计
,如何设计![]() 的长度,才能确保无论
的长度,才能确保无论![]() 的值为多少,总可以通过设置机器人乙的释放角度使之挑战成功?
的值为多少,总可以通过设置机器人乙的释放角度使之挑战成功?
(3)若![]() 与
与![]() 的夹角为
的夹角为![]() ,
,![]() 足够长,则如何设置机器人乙的释放角度,才能挑战成功?
足够长,则如何设置机器人乙的释放角度,才能挑战成功?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C的对边分别为a,b,c,且asinB=bsin(A+![]() ).
).
(1)求A;
(2)若b,![]() a,c成等差数列,△ABC的面积为2
a,c成等差数列,△ABC的面积为2![]() ,求a.
,求a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD是一个菱形,三角形PAD是一个等腰三角形,∠BAD=∠PAD=![]() ,点E在线段PC上,且PE=3EC.
,点E在线段PC上,且PE=3EC.
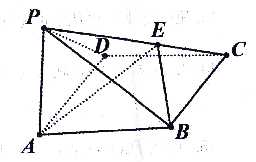
(1)求证:AD⊥PB;
(2)若平面PAD⊥平面ABCD,求二面角E﹣AB﹣P的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】类似于平面直角坐标系,我们可以定义平面斜坐标系:设数轴![]() 的交点为
的交点为![]() ,与
,与![]() 轴正方向同向的单位向量分别是
轴正方向同向的单位向量分别是![]() ,且
,且![]() 与
与![]() 的夹角为
的夹角为![]() ,其中
,其中![]() 。由平面向量基本定理,对于平面内的向量
。由平面向量基本定理,对于平面内的向量![]() ,存在唯一有序实数对
,存在唯一有序实数对![]() ,使得
,使得![]() ,把
,把![]() 叫做点
叫做点![]() 在斜坐标系
在斜坐标系![]() 中的坐标,也叫做向量
中的坐标,也叫做向量![]() 在斜坐标系
在斜坐标系![]() 中的坐标。在平面斜坐标系内,直线的方向向量、法向量、点方向式方程、一般式方程等概念与平面直角坐标系内相应概念以相同方式定义,如
中的坐标。在平面斜坐标系内,直线的方向向量、法向量、点方向式方程、一般式方程等概念与平面直角坐标系内相应概念以相同方式定义,如![]() 时,方程
时,方程![]() 表示斜坐标系内一条过点(2,1),且方向向量为(4,-5)的直线。
表示斜坐标系内一条过点(2,1),且方向向量为(4,-5)的直线。
(1)若![]() ,
,![]() ,且
,且![]() 与
与![]() 的夹角为锐角,求实数m的取值范围;
的夹角为锐角,求实数m的取值范围;
(2)若![]() ,已知点
,已知点![]() 和直线
和直线![]() ①求l的一个法向量;②求点A到直线l的距离。
①求l的一个法向量;②求点A到直线l的距离。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com