
分析 (1)利用同角三角函数的基本关系求得x为第四象限角,2sinxcosx=-$\frac{24}{25}$,再根据 sinx-cosx=-$\sqrt{{(sinx-cosx)}^{2}}$,计算求得结果.
(2)由条件求得sinx+cosx和sinx-cosx的值,可得sinx和cosx、tanx的值,从而求得要求式子的值.
解答 解:(1)∵-π<x<0,$sinx+cosx=\frac{1}{5}$,∴1+2sinxcosx=$\frac{1}{25}$,
∴2sinxcosx=-$\frac{24}{25}$,故x为第四象限角,sinx<0,cosx>0,
∴sinx-cosx=-$\sqrt{{(sinx-cosx)}^{2}}$=-$\sqrt{1-2sinxcosx}$=-$\frac{7}{5}$.
(2)由(1)可得sinx-cosx=-$\frac{7}{5}$,$sinx+cosx=\frac{1}{5}$,
∴sinx=-$\frac{3}{5}$,cosx=$\frac{4}{5}$,tanx=-$\frac{3}{4}$,
$\frac{3si{n}^{2}\frac{x}{2}-2sin\frac{x}{2}cos\frac{x}{2}+co{s}^{2}\frac{x}{2}}{tanx+\frac{1}{tanx}}$=$\frac{3•\frac{1-cosx}{2}-sinx+\frac{1+cosx}{2}}{tanx+\frac{1}{tanx}}$=$\frac{2-cosx-sinx}{tanx+\frac{1}{tanx}}$
=$\frac{2-\frac{4}{5}+\frac{3}{5}}{-\frac{3}{4}-\frac{4}{3}}$=-$\frac{108}{125}$.
点评 本题主要考查同角三角函数的基本关系的应用,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{1}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $144+2\sqrt{10}π$ | B. | $144+({2\sqrt{10}-2})π$ | C. | $128+2\sqrt{10}π$ | D. | $128+({2\sqrt{10}-2})π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
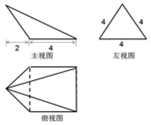
| A. | $\frac{32}{3}$ | B. | $\frac{{16\sqrt{3}}}{3}$ | C. | $\frac{{32\sqrt{3}}}{3}$ | D. | $\frac{{64\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 支持 | 无所谓 | 反对 | |
| 高一年级 | 18 | x | 2 |
| 高二年级 | 10 | 6 | y |
| 高一年级 | 高二年级 | 总计 | |
| 支持 | |||
| 不支持 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.01 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com