
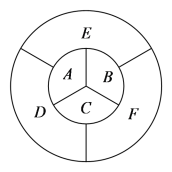
【题目】如下图中![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 六个区域进行染色,每个区域只染一种颜色,每个区域只染一种颜色,且相邻的区域不同色.若有
六个区域进行染色,每个区域只染一种颜色,每个区域只染一种颜色,且相邻的区域不同色.若有![]() 种颜色可供选择,则共有_________种不同的染色方案.
种颜色可供选择,则共有_________种不同的染色方案.
【答案】![]()
【解析】
通过分析题目给出的图形,可知要完成给出的图形中![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 六个区域进行染色,最少需要
六个区域进行染色,最少需要![]() 种颜色,即
种颜色,即![]() 同色,
同色,![]() 同色,
同色,![]() 同色,由排列知识可得该类染色方法的种数;也可以
同色,由排列知识可得该类染色方法的种数;也可以![]() 种颜色全部用上,即
种颜色全部用上,即![]() 、
、![]() 、
、![]() 三组中有一组不同色,同样利用排列组合知识求解该类染色方法的种数,最后利用分类加法求和即可.
三组中有一组不同色,同样利用排列组合知识求解该类染色方法的种数,最后利用分类加法求和即可.
要完成给出的图形中![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 六个区域进行染色,
六个区域进行染色,
染色方法分为两类,第一类是仅用三种颜色染色,
即![]() 同色,
同色,![]() 同色,
同色,![]() 同色,即从四种颜色中取三种颜色,有
同色,即从四种颜色中取三种颜色,有![]() 种取法,三种颜色染三个区域有
种取法,三种颜色染三个区域有![]() 种染法,共
种染法,共![]() 种染法;
种染法;
第二类是用四种颜色染色,即![]() 、
、![]() 、
、![]() 三组中有一组不同色,则有
三组中有一组不同色,则有![]() 种方案(
种方案(![]() 不同色或
不同色或![]() 不同色或
不同色或![]() 不同色),
不同色),
先从四种颜色中取两种染同色区域有![]() 种染法,剩余两种染在不同色区域有
种染法,剩余两种染在不同色区域有![]() 种染法,
种染法,
共有![]() 种染法.
种染法.
由分类加法原理可得总的染色方法种数为![]() (种).
(种).
故答案为:![]() .
.


科目:高中数学 来源: 题型:
【题目】某医务人员说:“包括我在内,我们社区诊所医生和护士共有16名.无论是否把我算在内,下面说法都是对的.在这些医务人员中:护士多于医生;女医生多于女护士;女护士多于男护士;至少有一名男医生.”请你推断说话的人的性别与职业是( )
A.男医生B.女医生C.男护士D.女护士
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知顶点为原点的抛物线C的焦点与椭圆![]() 的上焦点重合,且过点
的上焦点重合,且过点![]() .
.
(1)求椭圆的标准方程;
(2)若抛物线上不同两点A,B作抛物线的切线,两切线的斜率![]() ,若记AB的中点的横坐标为m,AB的弦长
,若记AB的中点的横坐标为m,AB的弦长![]() ,并求
,并求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的普通方程为
的普通方程为![]() .在以坐标原点为极点,
.在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出圆![]() 的参数方程和直线
的参数方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 在
在![]() 上,点Q在
上,点Q在![]() 上,求
上,求![]() 的最小值及此时点
的最小值及此时点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】河北省高考综合改革从2018年秋季入学的高一年级学生开始实施,新高考将实行“3+1+2”模式,其中3表示语文、数学、外语三科必选,1表示从物理、历史两科中选择一科,2表示从化学、生物、政治、地理四科中选择两科.某校2018级入学的高一学生选科情况如下表:
选科组合 | 物化生 | 物化政 | 物化地 | 物生政 | 物生地 | 物政地 | 史政地 | 史政化 | 史生政 | 史地化 | 史地生 | 史化生 | 合计 |
男 | 130 | 45 | 55 | 30 | 25 | 15 | 30 | 10 | 40 | 10 | 15 | 20 | 425 |
女 | 100 | 45 | 50 | 35 | 35 | 35 | 40 | 20 | 55 | 15 | 25 | 20 | 475 |
合计 | 230 | 90 | 105 | 65 | 60 | 50 | 70 | 30 | 95 | 25 | 40 | 40 | 900 |
(1)完成下面的![]() 列联表,并判断是否在犯错误概率不超过0.01的前提下,认为“选择物理与学生的性别有关”?
列联表,并判断是否在犯错误概率不超过0.01的前提下,认为“选择物理与学生的性别有关”?
(2)以频率估计概率,从该校2018级高一学生中随机抽取3名同学,设这三名同学中选择物理的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
选择物理 | 不选择物理 | 合计 | |
男 | 425 | ||
女 | 475 | ||
合计 | 900 |
附表及公式: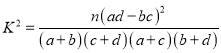
| 0.150 | 0.100 | 0.050 | 0.010 |
| 2.072 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程
的参数方程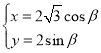 (
(![]() 为参数).直线
为参数).直线![]() 的参数方程
的参数方程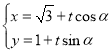 (
(![]() 为参数).
为参数).
(Ⅰ)求曲线![]() 在直角坐标系中的普通方程;
在直角坐标系中的普通方程;
(Ⅱ)以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,当曲线
轴的正半轴为极轴建立极坐标系,当曲线![]() 截直线
截直线![]() 所得线段的中点极坐标为
所得线段的中点极坐标为![]() 时,求直线
时,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com