
分析 a1=$\sqrt{3}$,an+1=$\frac{\sqrt{3}+{a}_{n}}{1-\sqrt{3}{a}_{n}}$(n∈N*),可得a2=-$\sqrt{3}$,a3=0,a4=$\sqrt{3}$,…,an+3=an.即可得出.
解答 解:∵a1=$\sqrt{3}$,an+1=$\frac{\sqrt{3}+{a}_{n}}{1-\sqrt{3}{a}_{n}}$(n∈N*),
∴a2=$\frac{\sqrt{3}+\sqrt{3}}{1-\sqrt{3}×\sqrt{3}}$=-$\sqrt{3}$,a3=$\frac{-\sqrt{3}+\sqrt{3}}{1-\sqrt{3}×(-\sqrt{3})}$=0,
a4=$\frac{\sqrt{3}+0}{1-0}$=$\sqrt{3}$,…,
∴an+3=an.
∴a1+a2+a3=0,
∴S2015=(a1+a2+a3)×671+a1+a2=0,
故答案为:0.
点评 本题考查了递推关系、数列的周期性,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | -$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
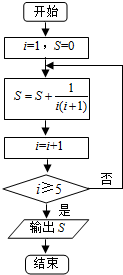
| A. | $\frac{4}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{5}{6}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30个 | B. | 35个 | C. | 20个 | D. | 15个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com