
分析 (1)由条件利用正弦函数的单调性求得函数f(x)的单调递增区间.
(2)令f(x)=0,求出 x的值,可得相邻的零点之间的间隔依次为$\frac{π}{3}$、$\frac{2π}{3}$.f(x)在[a,b]上至少含有6个零点,等价于b-a的最小值为2×$\frac{2π}{3}$+3×$\frac{π}{3}$.
解答 解:(1)对于函数f(x)=2sin(2x+$\frac{π}{3}$)+1,令2kπ-$\frac{π}{2}$≤2x+$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,k∈z,
求得kπ-$\frac{5π}{12}$≤x≤kπ+$\frac{π}{12}$,可得函数的增区间为[kπ-$\frac{5π}{12}$,kπ+$\frac{π}{12}$],k∈z.
(2)令f(x)=0,求出 sin(2x+$\frac{π}{3}$)=-$\frac{1}{2}$,∴x=kπ-$\frac{π}{4}$,或x=kπ-$\frac{7π}{12}$,
故相邻的零点之间的间隔依次为$\frac{π}{3}$、$\frac{2π}{3}$.
y=f(x)在[a,b]上至少含有6个零点,等价于b-a的最小值为 2×$\frac{2π}{3}$+3×$\frac{π}{3}$=$\frac{7π}{3}$.
点评 本题主要考查正弦函数的图象,正弦函数的单调性和零点,属于基础题.


科目:高中数学 来源: 题型:解答题
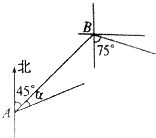 中国渔政310船在一次巡航执法作业中,发现在北偏东45°方向,相距12海里的水面上,有一艘不明国籍渔船正以每小时10海里的速度沿南偏东75°方向前进,中国渔政310船以每小时14海里的速度沿北偏东45°+α方向拦截该渔船,若要在最短的时间内拦截住,求中国渔政310船所需的时间和角α的正弦值.
中国渔政310船在一次巡航执法作业中,发现在北偏东45°方向,相距12海里的水面上,有一艘不明国籍渔船正以每小时10海里的速度沿南偏东75°方向前进,中国渔政310船以每小时14海里的速度沿北偏东45°+α方向拦截该渔船,若要在最短的时间内拦截住,求中国渔政310船所需的时间和角α的正弦值.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 16$\sqrt{3}$ | C. | 8 | D. | 8$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{π}{4}$,$\frac{π}{2}$) | B. | [$\frac{π}{4}$,$\frac{π}{2}$)∪($\frac{π}{2}$,π) | C. | [0,$\frac{π}{3}$]∪($\frac{2π}{3}$,π) | D. | [0,$\frac{π}{4}$]∪($\frac{π}{2}$,π) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{3}{2}$,+∞) | B. | (2,+∞) | C. | (0,$\frac{3}{2}$) | D. | ($\frac{3}{2}$,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (0,+∞) | C. | (-∞,1) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {x|-1≤x<2} | C. | {x|-2≤x<-1} | D. | {x|2≤x<3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com