
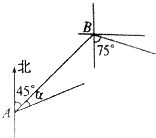
 中国渔政310船在一次巡航执法作业中,发现在北偏东45°方向,相距12海里的水面上,有一艘不明国籍渔船正以每小时10海里的速度沿南偏东75°方向前进,中国渔政310船以每小时14海里的速度沿北偏东45°+α方向拦截该渔船,若要在最短的时间内拦截住,求中国渔政310船所需的时间和角α的正弦值.
中国渔政310船在一次巡航执法作业中,发现在北偏东45°方向,相距12海里的水面上,有一艘不明国籍渔船正以每小时10海里的速度沿南偏东75°方向前进,中国渔政310船以每小时14海里的速度沿北偏东45°+α方向拦截该渔船,若要在最短的时间内拦截住,求中国渔政310船所需的时间和角α的正弦值. 分析 设中国渔政310船经过x小时后在C处追上渔船,利用余弦定理、正弦定理,即可得出结论.
解答  解:如图,设中国渔政310船经过x小时后在C处追上渔船,
解:如图,设中国渔政310船经过x小时后在C处追上渔船,
则AC=14x,BC=10x,∠ABC=120°,
根据余弦定理可得(14x)2=122+(10x)2-240xcos120°,
∴x=2,
∴AC=28,BC=20,
根据正弦定理得$\frac{BC}{sinα}=\frac{AC}{sin120°}$,
∴sinα=$\frac{5\sqrt{3}}{14}$,
∴中国渔政310船经过2小时后在C处追上渔船,角α的正弦值为$\frac{5\sqrt{3}}{14}$.
点评 本题考查利用数学知识解决实际问题,考查余弦定理、正定理的运用,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com