练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．（1）把5本不同的书分给3名同学，每人一本，有多少种不同的分法？
    （2）把5本相同的书分给3名同学，每人一本，有多少种不同的分法？

    分析 （1）5本不同的书分给3个同学，每人一本，从5本从选3本，分配给名同学，问题得以解决；
    （2）5本相同的书分给3名同学，每人一本，只有1种分法，问题得以解决．

    解答 解（1）5本不同的书分给3个同学，每人一本，所有的不同分法种数有A53=60；
    （2）5本相同的书分给3名同学，每人一本，只有1种分法．

    点评 本题主要考查了简单的排列组合，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    17．有5人担任5种不同的工作，现需调整，调整后至少有2人与原来工作不同，则不同的调整方法有119 种．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．在平行四边形ABCD中，AB=4，AD=2，E，F分别是BC，CD的中点，且$\overrightarrow{DE}•\overrightarrow{BF}$=-15，则∠ABC=60°．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知向量$\overrightarrow{i}$，$\overrightarrow{j}$，$\overrightarrow{k}$是空间直角坐标系Oxyz中，x轴，y轴，z轴正方向上的单位向量且$\overrightarrow{AB}$=-$\overrightarrow{i}$+$\overrightarrow{j}$-$\overrightarrow{k}$，则B的坐标是（-1，1，-1）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．平面直角坐标系中，O为坐标原点，设向量$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，其中$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（2，1），平面区域D由所有满足$\overrightarrow{OP}$=λ$\overrightarrow{a}$+μ$\overrightarrow{b}$，（0≤μ≤λ≤1）的点P（x，y）组成，点P使得z=ax+by（a＞0，b＞0）取得最大值3，则$\frac{1}{a}$+$\frac{2}{b}$的最小值是（　　）
    A．3+2$\sqrt{2}$B．4$\sqrt{2}$C．2D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

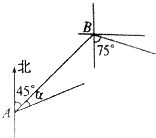    12．中国渔政310船在一次巡航执法作业中，发现在北偏东45°方向，相距12海里的水面上，有一艘不明国籍渔船正以每小时10海里的速度沿南偏东75°方向前进，中国渔政310船以每小时14海里的速度沿北偏东45°+α方向拦截该渔船，若要在最短的时间内拦截住，求中国渔政310船所需的时间和角α的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知数列{bn}满足b1=1，b2=5，bn+1=5bn-6bn-1，若数列{an}满足a1=1，an=bn（$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n-1}}$）（n≥2，n∈N*）．
    （1）求证：数列{bn+1-3bn}为等比数列，并求{bn}的通项公式；
    （2）求证：（1+$\frac{1}{{a}_{1}}$）（1+$\frac{1}{{a}_{2}}$）（1+$\frac{1}{{a}_{3}}$）…（1+$\frac{1}{{a}_{n}}$）＜3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．已知函数f（x）=sinx+$\sqrt{3}$cosx，则下列命题正确的是①③④．（填上你认为正确的所有命题的序号）
    ①函数f（x）（x∈[0，$\frac{π}{2}$]）的单调递增区间是[0，$\frac{π}{6}$]；
    ②函数f（x）的图象关于点（-$\frac{π}{6}$，0）对称；
    ③函数f（x）的图象向左平移m（m＞0）个单位长度后，所得的图象关于y轴对称，则m的最小值是$\frac{π}{6}$；
    ④若实数m使得方程f（x）=m在[0，2π]上恰好有三个实数解x1，x2，x3，则x1+x2+x3=$\frac{7π}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．已知数列{an}的前n项和为Sn=n（2n+1），则a10=39．

    查看答案和解析>>

    同步练习册答案