
分析 ①通过判断分母的单调性,从而判断函数f(x)的值域,②根据二次函数的性质判断即可;
③通过讨论x的范围,求出函数的对称轴,从而求出函数的递增区间;④根据相等函数的定义进行判断即可.
解答 解:①f(x)=$\frac{1}{{(x-1)}^{2}+1}$,
当x=1时,f(x)max=1,当x→∞时,f(x)→0,
∴函数f(x)的值域是:(0,1];
故①正确;
②若二次函数f(x)=ax2+bx+2没有零点,
即f(x)和x轴无交点,
则△=b2-8a<0,
故②错误;
③x≥0时,y=x2-2x-3,对称轴x=1,开口向上,
∴递增区间是[1,+∞),
x<0时,y=x2+2x-3,对称轴x=-1,开口向上,
∴递增区间是:[-1,0),
故③错误;
④函数$y=\sqrt{x+1}•\sqrt{x-1}$的定义域是:{x|x≥1},
$y=\sqrt{{x^2}-1}$的定义域是:{x|x≥1或x≤-1},
故不是相同的函数,
故④错误;
故答案为:①.
点评 本题考查了本题考查了函数的定义域,值域问题,考查函的单调性问题,是一道综合题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,3] | B. | [-1,8] | C. | [1,2] | D. | [-2,-1]∪[1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
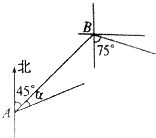 中国渔政310船在一次巡航执法作业中,发现在北偏东45°方向,相距12海里的水面上,有一艘不明国籍渔船正以每小时10海里的速度沿南偏东75°方向前进,中国渔政310船以每小时14海里的速度沿北偏东45°+α方向拦截该渔船,若要在最短的时间内拦截住,求中国渔政310船所需的时间和角α的正弦值.
中国渔政310船在一次巡航执法作业中,发现在北偏东45°方向,相距12海里的水面上,有一艘不明国籍渔船正以每小时10海里的速度沿南偏东75°方向前进,中国渔政310船以每小时14海里的速度沿北偏东45°+α方向拦截该渔船,若要在最短的时间内拦截住,求中国渔政310船所需的时间和角α的正弦值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com