Question

14．已知f（x）=ax²+bx（a≠0），若-1≤f（-1）≤2，2≤f（1）≤4且ac²+bc-b=0（a，b，c∈R），则实数c的取值范围是[$\frac{-3-\sqrt{21}}{2}$，$\frac{-3+\sqrt{21}}{2}$]．

Answer 1

分析 由已知-1≤f（-1）≤2，2≤f（1）≤4，利用线性规划可得：a∈[$\frac{1}{2}$，3]，b∈[0，$\frac{5}{2}$]，$\frac{b}{a}$∈[0，3]，又由ac²+bc-b=0可得：c＜1，$\frac{b}{a}$（c-1）≥3（c-1），整理得：c²+3c-3≤0，解得实数c的取值范围．

解答 解：∵f（x）=ax²+bx（a≠0），若-1≤f（-1）≤2，2≤f（1）≤4
∴$\left\{\begin{array}{l}-1≤a-b≤2\\ 2≤a+b≤4\end{array}\right.$，
其对应的平面区域如下图所示：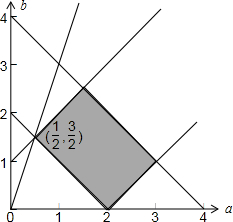

由图可知：a∈[$\frac{1}{2}$，3]，b∈[0，$\frac{5}{2}$]，$\frac{b}{a}$∈[0，3]
又∵且ac²+bc-b=0，则当c≥1时，ac²+bc-b≥a不成立，故c＜1，
则$\frac{b}{a}$（c-1）≥3（c-1），
即c²+$\frac{b}{a}$c-$\frac{b}{a}$≥c²+3c-3，
即ac²+bc-b=0≥a（c²+3c-3）
即c²+3c-3≤0，
解得：c∈[$\frac{-3-\sqrt{21}}{2}$，$\frac{-3+\sqrt{21}}{2}$]，
故答案为：[$\frac{-3-\sqrt{21}}{2}$，$\frac{-3+\sqrt{21}}{2}$]

点评 本题考查的知识点是二次函数的图象和性质，线性规划，本题转化困难，属于难题．