
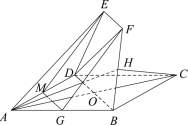
【题目】如图,正方形![]() 和梯形
和梯形![]() 所在的平面互相垂直,
所在的平面互相垂直,![]() ,
,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 的中点.
的中点.

(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)若![]() ,求证:平面
,求证:平面![]() 平面
平面![]() .
.
【答案】详见解析
【解析】
(Ⅰ)推导出AC⊥BD,从而AC⊥平面BDEF,由此能证明AC⊥BF;
(Ⅱ)法一:取AD中点M,连接ME,MG,则GM∥BD且![]() ,从而GM∥EF且GM=EF,进而四边形GMEF为平行四边形,从而GF∥ME,由此能证明GF∥平面ADE;
,从而GM∥EF且GM=EF,进而四边形GMEF为平行四边形,从而GF∥ME,由此能证明GF∥平面ADE;
法二:连接OF,OG,推导出四边形DOFE为平行四边形,从而OF∥DE,进而OF∥平面ADE,由O,G分别为BD,AB的中点,得OG∥AD,从而OG∥平面ADE,进而平面GOF∥平面ADE,由此能证明GF∥平面ADE;
(Ⅲ)连接OH,则OH∥DF,由DF⊥BF,得OH⊥BF,再由BF⊥AC,得BF⊥平面AHC,由此能证明平面AHC⊥平面BGF.
解:(Ⅰ)因为![]() 为正方形,所以
为正方形,所以![]() .又因为平面
.又因为平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .又因为
.又因为![]() 平面
平面![]() ,
,
所以![]() .
.
(Ⅱ)方法一:取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,
所以![]() 且
且![]() .又因为
.又因为![]() 且
且![]() ,
,
所以![]() 且
且![]() .所以四边形
.所以四边形![]() 为平行四边形.
为平行四边形.
所以![]() .因为
.因为![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
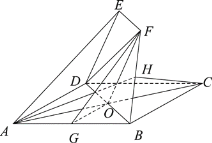
方法二:连接![]() ,
,![]() ,
,
因为![]() 且
且![]() ,
,
所以![]() 且
且![]() .
.
所以四边形![]() 为平行四边形.所以
为平行四边形.所以![]() .
.
因为![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .因为
.因为![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,
所以![]() .又因为
.又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .因为
.因为![]() ,
,
所以平面![]() 平面
平面![]() .因为
.因为![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
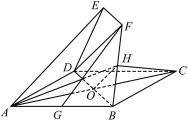
(Ⅲ)连接![]() ,
,
在![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,
所以![]() .因为
.因为![]() ,
,
所以![]() .因为
.因为![]() ,
,
![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .因为
.因为![]() 平面
平面![]() ,
,
所以平面![]()
![]() 平面
平面![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线
的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线![]() :
: ![]() 与椭圆
与椭圆![]() 有且只有一个公共点.
有且只有一个公共点.
(Ⅰ)求椭圆![]() 的方程及点
的方程及点![]() 的坐标;
的坐标;
(Ⅱ)设![]() 是坐标原点,直线
是坐标原点,直线![]() 平行于
平行于![]() ,与椭圆
,与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,且与直线
,且与直线![]() 交于点
交于点![]() ,证明:存在常数
,证明:存在常数![]() ,使得
,使得![]() ,并求
,并求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】部分与整体以某种相似的方式呈现称为分形,一个数学意义上分形的生成是基于一个不断迭代的方程式,即一种基于递归的反馈系统.分形几何学不仅让人们感悟到科学与艺木的融合,数学与艺术审美的统一,而且还有其深刻的科学方法论意义.如图,由波兰数学家谢尔宾斯基1915年提出的谢尔宾斯基三角形就属于-种分形,具体作法是取一个实心三角形,沿三角形的三边中点连线,将它分成4个小三角形,去掉中间的那一个小三角形后,对其余3个小三角形重复上述过程逐次得到各个图形.

若在图④中随机选取-点,则此点取自阴影部分的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,则“存在常数
,则“存在常数![]() ,对任意的
,对任意的![]() ,且
,且![]() ,都有
,都有![]() ”是“数列
”是“数列![]() 为等差数列”的( )
为等差数列”的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年1月22日,依照中国文联及中国民间文艺家协会命名中国观音文化之乡的有关规定,中国文联、中国民协正式命名四川省遂宁市为“中国观音文化之乡”.
下表为2014年至2018年观音文化故里某土特产企业的线下销售额(单位:万元)
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
线下销售额 | 90 | 170 | 210 | 280 | 340 |
为了解“祝福观音、永保平安”活动的支持度.某新闻调查组对40位老年市民和40位年轻市民进行了问卷调查(每位市民从“很支持”和“支持”中任选一种),其中很支持的老年市民有30人,支持的年轻市民有15人.
(1)从以上5年中任选2年,求其销售额均超过200万元的概率;
(2)请根据以上信息列出列联表,并判断能否有85%的把握认为支持程度与年龄有关.
附:![]() ,其中
,其中![]()
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com