
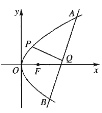
【题目】已知![]() 是抛物线
是抛物线![]() 的焦点,点
的焦点,点![]() 是抛物线上一点,且
是抛物线上一点,且![]() ,直线
,直线![]() 过定点(4,0),与抛物线
过定点(4,0),与抛物线![]() 交于
交于![]() 两点,点
两点,点![]() 在直线
在直线![]() 上的射影是
上的射影是![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;
;![]() (2)
(2)![]()
【解析】
(1)根据抛物线上的点到抛物线焦点的距离等于该点到抛物线准线的距离求解![]() 的值,进而根据点在抛物线上求解
的值,进而根据点在抛物线上求解![]() 的值;(2)联立直线与抛物线的方程得到一元二次方程,利用韦达定理结合两直线垂直或线段的长度的关系求解参数的值,进而确定直线方程.
的值;(2)联立直线与抛物线的方程得到一元二次方程,利用韦达定理结合两直线垂直或线段的长度的关系求解参数的值,进而确定直线方程.
解:(1)由![]() 得
得![]() ,所以
,所以![]() ,
,
将![]() 代入
代入![]() ,得
,得![]() .
.
(2)解法一:因为![]() ,由(1)知点
,由(1)知点![]() ,
,
抛物线![]() 的方程为
的方程为![]() ,
,
设直线![]() 的方程是
的方程是![]() ,
,
由![]() 得
得![]() ,
,
设![]() ,
,
则![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() ,且
,且![]() ,
,
所以![]() ,
,
且![]() ,
,
由![]() ,
,
得![]() ,
,
即![]() ,
,
![]() ,
,
解得![]() (舍去)或
(舍去)或![]() ,
,
所以直线![]() 的方程是
的方程是![]() ,
,
即![]() .
.
解法二:因为![]() ,由(1)知点
,由(1)知点![]() ,
,
抛物线![]() 的方程为
的方程为![]() ,
,
设直线![]() 的方程是
的方程是![]() ,
,
由![]() 得
得![]() ,
,
设![]() ,
,
则![]() ,
,
由![]()
解得![]() 点的纵坐标是
点的纵坐标是![]() ,
,
![]() ,
,
![]()
![]() ,
,
因为![]() ,
,
所以![]()
 ,
,
化简得![]() ,
,
解得![]() (舍去)或
(舍去)或![]() ,
,
所以直线![]() 的方程是
的方程是![]() ,
,
即![]()


科目:高中数学 来源: 题型:
【题目】(1)某中学理学社为了吸收更多新社员,在校团委的支持下,在高一学年组织了抽签赠书活动.月初报名,月末抽签,最初有30名同学参加.社团活动积极分子甲同学参加了活动.
①第一个月有18个中签名额.甲先抽签,乙和丙紧随其后抽签.求这三名同学同时中签的概率.
②理学社设置了第![]() (
(![]() )个月中签的名额为
)个月中签的名额为![]() ,并且抽中的同学退出活动,同时补充新同学,补充的同学比中签的同学少2个,如果某次抽签的同学全部中签,则活动立刻结束.求甲同学参加活动时间的期望.
,并且抽中的同学退出活动,同时补充新同学,补充的同学比中签的同学少2个,如果某次抽签的同学全部中签,则活动立刻结束.求甲同学参加活动时间的期望.
(2)某出版集团为了扩大影响,在全国组织了抽签赠书活动.报名和抽签时间与(1)中某中学理学社的报名和抽签时间相同,最初有30万人参加,甲同学在其中.每个月抽中的人退出活动,同时补充新人,补充的人数与中签的人数相同.出版集团设置了第![]() (
(![]() )个月中签的概率为
)个月中签的概率为![]() ,活动进行了
,活动进行了![]() 个月,甲同学很幸运,中签了,在此条件下,求证:甲同学参加活动时间的均值小于
个月,甲同学很幸运,中签了,在此条件下,求证:甲同学参加活动时间的均值小于![]() 个月.
个月.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面α∩平面β=l,A,C是α内不同的两点,B,D是β内不同的两点,且A,B,C,D直线l,M,N分别是线段AB,CD的中点.下列判断正确的是( )

A.若AB![]() CD,则MN
CD,则MN![]() l
l
B.若M,N重合,则AC![]() l
l
C.若AB与CD相交,且AC![]() l,则BD可以与l相交
l,则BD可以与l相交
D.若AB与CD是异面直线,则MN不可能与l平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】哈三中总务处的老师要购买学校教学用的粉笔,并且有非常明确的判断一盒粉笔是“优质产品”和“非优质产品”的方法.某品牌的粉笔整箱出售,每箱共有20盒,根据以往的经验,其中会有某些盒的粉笔为非优质产品,其余的都为优质产品.并且每箱含有0,1,2盒非优质产品粉笔的概率为0.7,0.2和0.1.为了购买该品牌的粉笔,校总务主任设计了一种购买的方案:欲买一箱粉笔,随机查看该箱的4盒粉笔,如果没有非优质产品,则购买,否则不购买.设“买下所查看的一箱粉笔”为事件![]() ,“箱中有
,“箱中有![]() 件非优质产品”为事件
件非优质产品”为事件![]() .
.
(1)求![]() ,
,![]() ,
,![]() ;
;
(2)随机查看该品牌粉笔某一箱中的四盒,设![]() 为非优质产品的盒数,求
为非优质产品的盒数,求![]() 的分布列及期望;
的分布列及期望;
(3)若购买100箱该品牌粉笔,如果按照主任所设计方案购买的粉笔中,箱中每盒粉笔都是优质产品的箱数的期望比随机购买的箱中每盒粉笔都是优质产品的箱数的期望大10,则所设计的方案有效.讨论该方案是否有效.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某水果批发商经销某种水果(以下简称![]() 水果),购入价为300元/袋,并以360元/袋的价格售出,若前8小时内所购进的
水果),购入价为300元/袋,并以360元/袋的价格售出,若前8小时内所购进的![]() 水果没有售完,则批发商将没售完的
水果没有售完,则批发商将没售完的![]() 水果以220元/袋的价格低价处理完毕(根据经验,2小时内完全能够把
水果以220元/袋的价格低价处理完毕(根据经验,2小时内完全能够把![]() 水果低价处理完,且当天不再购入).该水果批发商根据往年的销量,统计了100天
水果低价处理完,且当天不再购入).该水果批发商根据往年的销量,统计了100天![]() 水果在每天的前8小时内的销售量,制成如下频数分布条形图.
水果在每天的前8小时内的销售量,制成如下频数分布条形图.

记![]() 表示
表示![]() 水果一天前8小时内的销售量,
水果一天前8小时内的销售量,![]() 表示水果批发商一天经营
表示水果批发商一天经营![]() 水果的利润,
水果的利润,![]() 表示水果批发商一天批发
表示水果批发商一天批发![]() 水果的袋数.
水果的袋数.
(1)若![]() ,求
,求![]() 与
与![]() 的函数解析式;
的函数解析式;
(2)假设这100天中水果批发商每天购入![]() 水果15袋或者16袋,分别计算该水果批发商这100天经营
水果15袋或者16袋,分别计算该水果批发商这100天经营![]() 水果的利润的平均数,以此作为决策依据,每天应购入
水果的利润的平均数,以此作为决策依据,每天应购入![]() 水果15袋还是16袋?
水果15袋还是16袋?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为进一步深化“平安校园”创建活动,加强校园安全教育宣传,某高中对该校学生进行了安全教育知识测试(满分100分),并从中随机抽取了200名学生的成绩,经过数据分析得到如图1所示的频数分布表,并绘制了得分在![]() 以及
以及![]() 的茎叶图,分别如图23所示.
的茎叶图,分别如图23所示.
成绩 |
|
|
|
|
|
|
|
频数 | 5 | 30 | 40 | 50 | 45 | 20 | 10 |
图1
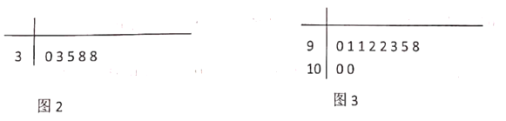
(1)求这200名同学得分的平均数;(同组数据用区间中点值作代表)
(2)如果变量![]() 满足
满足![]() 且
且![]() ,则称变量
,则称变量![]() “近似满足正态分布
“近似满足正态分布![]() 的概率分布”.经计算知样本方差为210,现在取
的概率分布”.经计算知样本方差为210,现在取![]() 和
和![]() 分别为样本平均数和方差,以样本估计总体,将频率视为概率,如果该校学生的得分“近似满足正态分布
分别为样本平均数和方差,以样本估计总体,将频率视为概率,如果该校学生的得分“近似满足正态分布![]() 的概率分布”,则认为该校的校园安全教育是成功的,否则视为不成功.试判断该校的安全教育是否成功,并说明理由.
的概率分布”,则认为该校的校园安全教育是成功的,否则视为不成功.试判断该校的安全教育是否成功,并说明理由.
(3)学校决定对90分及以上的同学进行奖励,为了体现趣味性,采用抽奖的方式进行,其中得分不低于94的同学有两次抽奖机会,低于94的同学只有一次抽奖机会,每次抽奖的奖金及对应的概率分别为:
奖金 | 50 | 100 |
概率 |
|
|
现在从不低于90同学中随机选一名同学,记其获奖金额为![]() ,以样本估计总体,将频率视为概率,求
,以样本估计总体,将频率视为概率,求![]() 的分布列和数学期望.
的分布列和数学期望.
(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,圆
,圆![]() :
:![]() ,一动圆在
,一动圆在![]() 轴右侧与
轴右侧与![]() 轴相切,同时与圆
轴相切,同时与圆![]() 相外切,此动圆的圆心轨迹为曲线
相外切,此动圆的圆心轨迹为曲线![]() ,椭圆
,椭圆![]() 与曲线
与曲线![]() 有相同的焦点.
有相同的焦点.
(1)求曲线![]() 的方程;
的方程;
(2)设曲线![]() 与椭圆
与椭圆![]() 相交于第一象限点
相交于第一象限点![]() ,且
,且![]() ,求椭圆
,求椭圆![]() 的标准方程;
的标准方程;
(3)在(2)的条件下,如果椭圆![]() 的左顶点为
的左顶点为![]() ,过
,过![]() 且垂直于
且垂直于![]() 轴的直线与椭圆
轴的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() ,
,![]() 与直线
与直线![]() :
:![]() 分别交于
分别交于![]() ,
,![]() 两点,证明:四边形
两点,证明:四边形![]() 的对角线的交点是椭圆
的对角线的交点是椭圆![]() 的右顶点.
的右顶点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着疫情的有效控制,人们的生产生活逐渐向正常秩序恢复,位于我区的某著名赏花园区重新开放.据统计硏究,近期每天赏花的人数大致符合以下数学模型![]() .以
.以 表示第
表示第![]() 个时刻进入园区的人数,以
个时刻进入园区的人数,以 表示第
表示第![]() 个时刻离开园区的人数,设定每15分钟为一个计算单位,上午8点15分作为第1个计算人数单位,即
个时刻离开园区的人数,设定每15分钟为一个计算单位,上午8点15分作为第1个计算人数单位,即![]() 点30分作为第2个计算单位,即
点30分作为第2个计算单位,即![]() :依次类推,把一天内从上午8点到下午5点分成36个计算单位(最后结果四舍五入,精确到整数)
:依次类推,把一天内从上午8点到下午5点分成36个计算单位(最后结果四舍五入,精确到整数)
(1)试分别计算当天12:30至13:30这一小时内,进入园区的人数![]() 和离开园区的游客人数
和离开园区的游客人数![]() .
.
(2)请问,从12点(即![]() )开始,园区内总人数何时达到最多?并说明理由
)开始,园区内总人数何时达到最多?并说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com