
ЁОЬтФПЁПФГЫЎЙћХњЗЂЩЬОЯњФГжжЫЎЙћЃЈвдЯТМђГЦ![]() ЫЎЙћЃЉЃЌЙКШыМлЮЊ300дЊ/ДќЃЌВЂвд360дЊ/ДќЕФМлИёЪлГіЃЌШєЧА8аЁЪБФкЫљЙКНјЕФ
ЫЎЙћЃЉЃЌЙКШыМлЮЊ300дЊ/ДќЃЌВЂвд360дЊ/ДќЕФМлИёЪлГіЃЌШєЧА8аЁЪБФкЫљЙКНјЕФ![]() ЫЎЙћУЛгаЪлЭъЃЌдђХњЗЂЩЬНЋУЛЪлЭъЕФ
ЫЎЙћУЛгаЪлЭъЃЌдђХњЗЂЩЬНЋУЛЪлЭъЕФ![]() ЫЎЙћвд220дЊ/ДќЕФМлИёЕЭМлДІРэЭъБЯЃЈИљОнОбщЃЌ2аЁЪБФкЭъШЋФмЙЛАб
ЫЎЙћвд220дЊ/ДќЕФМлИёЕЭМлДІРэЭъБЯЃЈИљОнОбщЃЌ2аЁЪБФкЭъШЋФмЙЛАб![]() ЫЎЙћЕЭМлДІРэЭъЃЌЧвЕБЬьВЛдйЙКШыЃЉ.ИУЫЎЙћХњЗЂЩЬИљОнЭљФъЕФЯњСПЃЌЭГМЦСЫ100Ьь
ЫЎЙћЕЭМлДІРэЭъЃЌЧвЕБЬьВЛдйЙКШыЃЉ.ИУЫЎЙћХњЗЂЩЬИљОнЭљФъЕФЯњСПЃЌЭГМЦСЫ100Ьь![]() ЫЎЙћдкУПЬьЕФЧА8аЁЪБФкЕФЯњЪлСПЃЌжЦГЩШчЯТЦЕЪ§ЗжВМЬѕаЮЭМ.
ЫЎЙћдкУПЬьЕФЧА8аЁЪБФкЕФЯњЪлСПЃЌжЦГЩШчЯТЦЕЪ§ЗжВМЬѕаЮЭМ.

МЧ![]() БэЪО
БэЪО![]() ЫЎЙћвЛЬьЧА8аЁЪБФкЕФЯњЪлСПЃЌ
ЫЎЙћвЛЬьЧА8аЁЪБФкЕФЯњЪлСПЃЌ![]() БэЪОЫЎЙћХњЗЂЩЬвЛЬьОгЊ
БэЪОЫЎЙћХњЗЂЩЬвЛЬьОгЊ![]() ЫЎЙћЕФРћШѓЃЌ
ЫЎЙћЕФРћШѓЃЌ![]() БэЪОЫЎЙћХњЗЂЩЬвЛЬьХњЗЂ
БэЪОЫЎЙћХњЗЂЩЬвЛЬьХњЗЂ![]() ЫЎЙћЕФДќЪ§.
ЫЎЙћЕФДќЪ§.
ЃЈ1ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() гы
гы![]() ЕФКЏЪ§НтЮіЪНЃЛ
ЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉМйЩшет100ЬьжаЫЎЙћХњЗЂЩЬУПЬьЙКШы![]() ЫЎЙћ15ДќЛђеп16ДќЃЌЗжБ№МЦЫуИУЫЎЙћХњЗЂЩЬет100ЬьОгЊ
ЫЎЙћ15ДќЛђеп16ДќЃЌЗжБ№МЦЫуИУЫЎЙћХњЗЂЩЬет100ЬьОгЊ![]() ЫЎЙћЕФРћШѓЕФЦНОљЪ§ЃЌвдДЫзїЮЊОіВпвРОнЃЌУПЬьгІЙКШы
ЫЎЙћЕФРћШѓЕФЦНОљЪ§ЃЌвдДЫзїЮЊОіВпвРОнЃЌУПЬьгІЙКШы![]() ЫЎЙћ15ДќЛЙЪЧ16ДќЃП
ЫЎЙћ15ДќЛЙЪЧ16ДќЃП
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ15Дќ
ЃЛЃЈ2ЃЉ15Дќ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОн![]() ЃЌЗж
ЃЌЗж![]() ЃЌ
ЃЌ![]() ЃЌгЩРћШѓКЏЪ§ЧѓНт.
ЃЌгЩРћШѓКЏЪ§ЧѓНт.
ЃЈ2ЃЉШєЫЎЙћХњЗЂЩЬУПЬьЙКШы![]() ЫЎЙћ15ДќЃЌИљОнЭГМЦЭМЃЌдђет100Ььжага80ЬьЕФРћШѓЮЊ900дЊЃЌга20ЬьЕФРћШѓЮЊ760дЊЃЌЧѓЕУЦНОљЪ§ЃЌШєЫЎЙћХњЗЂЩЬУПЬьЙКШы
ЫЎЙћ15ДќЃЌИљОнЭГМЦЭМЃЌдђет100Ььжага80ЬьЕФРћШѓЮЊ900дЊЃЌга20ЬьЕФРћШѓЮЊ760дЊЃЌЧѓЕУЦНОљЪ§ЃЌШєЫЎЙћХњЗЂЩЬУПЬьЙКШы![]() ЫЎЙћ16ДќЃЌдђет100Ььжага50ЬьЕФРћШѓЮЊ960дЊЃЌга30ЬьЕФРћШѓЮЊ820дЊЃЌга20ЬьЕФРћШѓЮЊ680дЊЃЌдйЧѓЕУЦфЦНОљЪ§ЃЌСНепБШНЯЯТНсТл.
ЫЎЙћ16ДќЃЌдђет100Ььжага50ЬьЕФРћШѓЮЊ960дЊЃЌга30ЬьЕФРћШѓЮЊ820дЊЃЌга20ЬьЕФРћШѓЮЊ680дЊЃЌдйЧѓЕУЦфЦНОљЪ§ЃЌСНепБШНЯЯТНсТл.
ЃЈ1ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
злЩЯЃЌ![]() .
.
ЃЈ2ЃЉШєЫЎЙћХњЗЂЩЬУПЬьЙКШы![]() ЫЎЙћ15ДќЃЌдђет100Ььжага80ЬьЕФРћШѓЮЊ900дЊЃЌга20ЬьЕФРћШѓЮЊ760дЊЃЌ
ЫЎЙћ15ДќЃЌдђет100Ььжага80ЬьЕФРћШѓЮЊ900дЊЃЌга20ЬьЕФРћШѓЮЊ760дЊЃЌ
вђДЫИУЫЎЙћХњЗЂЩЬет100ЬьОгЊ![]() ЫЎЙћЕФРћШѓЕФЦНОљЪ§ЮЊ
ЫЎЙћЕФРћШѓЕФЦНОљЪ§ЮЊ![]() .
.
ШєЫЎЙћХњЗЂЩЬУПЬьЙКШы![]() ЫЎЙћ16ДќЃЌдђет100Ььжага50ЬьЕФРћШѓЮЊ960дЊЃЌга30ЬьЕФРћШѓЮЊ820дЊЃЌга20ЬьЕФРћШѓЮЊ680дЊЃЌ
ЫЎЙћ16ДќЃЌдђет100Ььжага50ЬьЕФРћШѓЮЊ960дЊЃЌга30ЬьЕФРћШѓЮЊ820дЊЃЌга20ЬьЕФРћШѓЮЊ680дЊЃЌ
вђДЫИУЫЎЙћХњЗЂЩЬет100ЬьОгЊ![]() ЫЎЙћЕФРћШѓЕФЦНОљЪ§ЮЊ
ЫЎЙћЕФРћШѓЕФЦНОљЪ§ЮЊ![]() .
.
БШНЯСНИіЦНОљЪ§ПЩжЊЃЌУПЬьгІЙКШы![]() ЫЎЙћ15Дќ.
ЫЎЙћ15Дќ.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЪЕЯжЙњМвИЛЧП.УёзхИДаЫ.ШЫУёавИЃЪЧЁАжаЙњУЮЁБЕФБОжЪФкК.ФГЩЬМвМЦЛЎвдЁАШЋУёНЁЩэДйНЁПЕЃЌЭЌаФЙВжўжаЙњУЮЁБЮЊжїЬтОйАьвЛДЮгаНБЯћЗбЛюЖЏЃЌДЫЩЬМвЯШАбФГЦЗХЦЦЙХвЧђжиаТАќзАЃЌАќзАЪБдкУПИіЦЙХвЧђЩЯгЁЩЯЁАжаЁБЁАЙњЁБЁАУЮЁБШ§ИізжбљжаЕФвЛИіЃЌжЎКѓЫцЛњзАКаЃЈ1Ка4ИіЧђЃЉЃЌВЂЙцЖЈЃКШєЙЫПЭЙКТђЕФвЛКаЧђгЁЕФЪЧЭЌвЛИізжЃЌдђДЫЙЫПЭЛёЕУвЛЕШНБЃЛШєЙЫПЭЙКТђЕФвЛКаЧђМЏЦыСЫЁАжаЁБЁАЙњЁБЖўзжЧвНігаДЫЖўзжЃЌдђДЫЙЫПЭЛёЕУЖўЕШНБЃЛШєЙЫПЭЙКТђЕФвЛКаЧђМЏЦыСЫЁАжаЁБЁАЙњЁБЁАУЮЁБШ§ИізжЃЌдђДЫЙЫПЭЛёЕУШ§ЕШНБЃЌЦфЫќЧщПіВЛЩшНБЃЌдђЙЫПЭЙКТђвЛКаЦЙХвЧђЛёНБЕФИХТЪЪЧ_____________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§Са{an}ЮЊе§ЯюЕШБШЪ§СаЃЌa1ЃН1ЃЌЪ§Са{bn}Тњзуb2ЃН3ЃЌa1b1+a2b2+a3b3+Ё+anbnЃН3+ЃЈ2nЉ3ЃЉ2nЃЎ
ЃЈ1ЃЉЧѓanЃЛ
ЃЈ2ЃЉЧѓ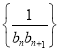 ЕФЧАnЯюКЭTnЃЎ
ЕФЧАnЯюКЭTnЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§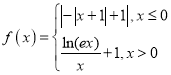 ЃЌШєЗНГЬ
ЃЌШєЗНГЬ![]() га7ИіВЛЭЌЕФЪЕЪ§Нт,дђ
га7ИіВЛЭЌЕФЪЕЪ§Нт,дђ![]() ЕФШЁжЕЗЖЮЇЃЈ ЃЉ
ЕФШЁжЕЗЖЮЇЃЈ ЃЉ
A.(2,6)B.(6,9)C.(2,12)D.(4,13)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
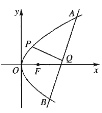
ЁОЬтФПЁПвбжЊ![]() ЪЧХзЮяЯп
ЪЧХзЮяЯп![]() ЕФНЙЕуЃЌЕу
ЕФНЙЕуЃЌЕу![]() ЪЧХзЮяЯпЩЯвЛЕуЃЌЧв
ЪЧХзЮяЯпЩЯвЛЕуЃЌЧв![]() ЃЌжБЯп
ЃЌжБЯп![]() Й§ЖЈЕуЃЈ4ЃЌ0ЃЉЃЌгыХзЮяЯп
Й§ЖЈЕуЃЈ4ЃЌ0ЃЉЃЌгыХзЮяЯп![]() НЛгк
НЛгк![]() СНЕуЃЌЕу
СНЕуЃЌЕу![]() дкжБЯп
дкжБЯп![]() ЩЯЕФЩфгАЪЧ
ЩЯЕФЩфгАЪЧ![]() .
.
ЃЈ1ЃЉЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧв
ЃЌЧв![]() ЃЌЧѓжБЯп
ЃЌЧѓжБЯп![]() ЕФЗНГЬ.
ЕФЗНГЬ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкМЋзјБъЯЕжаЃЌМЋЕуЮЊ![]() ЃЌвЛЬѕЗтБеЕФЧњЯп
ЃЌвЛЬѕЗтБеЕФЧњЯп![]() гЩЫФЖЮЧњЯпзщГЩЃК
гЩЫФЖЮЧњЯпзщГЩЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() .
.
ЃЈ1ЃЉЧѓИУЗтБеЧњЯпЫљЮЇГЩЕФЭМаЮУцЛ§ЃЛ
ЃЈ2ЃЉШєжБЯп![]() ЃК
ЃК![]() гыЧњЯп
гыЧњЯп![]() ЧЁга3ИіЙЋЙВЕуЃЌЧѓ
ЧЁга3ИіЙЋЙВЕуЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() ЃК
ЃК![]() ЕФРыаФТЪЮЊ
ЕФРыаФТЪЮЊ![]() ЃЌзѓгвЖЅЕуЗжБ№ЮЊ
ЃЌзѓгвЖЅЕуЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌгвНЙЕуЮЊ
ЃЌгвНЙЕуЮЊ![]() ЃЌ
ЃЌ![]() ЮЊЭждВЩЯвьгк
ЮЊЭждВЩЯвьгк![]() ЃЌ
ЃЌ![]() ЕФЖЏЕуЃЌЧв
ЕФЖЏЕуЃЌЧв![]() УцЛ§ЕФзюДѓжЕЮЊ
УцЛ§ЕФзюДѓжЕЮЊ![]() .
.
ЃЈ1ЃЉЧѓЭждВ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉЩшжБЯп![]() гы
гы![]() жсНЛгк
жсНЛгк![]() ЕуЃЌЙ§Еу
ЕуЃЌЙ§Еу![]() зї
зї![]() ЕФЦНааЯпНЛ
ЕФЦНааЯпНЛ![]() жсгыЕу
жсгыЕу![]() ЃЌЪдЬНОПЪЧЗёДцдкЖЈЕу
ЃЌЪдЬНОПЪЧЗёДцдкЖЈЕу![]() ЃЌЪЙЕУвд
ЃЌЪЙЕУвд![]() ЮЊжБОЖЕФдВКуЙ§ЖЈЕу
ЮЊжБОЖЕФдВКуЙ§ЖЈЕу![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
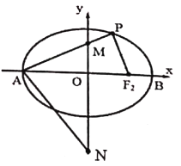
ЁОЬтФПЁПвбжЊЭждВ![]() ЕФРыаФТЪЮЊ
ЕФРыаФТЪЮЊ![]() ЃЌЧвЫФИіЖЅЕуЙЙГЩЕФЫФБпаЮЕФУцЛ§ЪЧ
ЃЌЧвЫФИіЖЅЕуЙЙГЩЕФЫФБпаЮЕФУцЛ§ЪЧ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓЭждВ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉвбжЊжБЯп![]() ОЙ§Еу
ОЙ§Еу![]() ЃЌЧвВЛДЙжБгк
ЃЌЧвВЛДЙжБгк![]() жсЃЌжБЯп
жсЃЌжБЯп![]() гыЭждВ
гыЭждВ![]() НЛгк
НЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌ
СНЕуЃЌ![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌжБЯп
ЕФжаЕуЃЌжБЯп![]() гыЭждВ
гыЭждВ![]() НЛгк
НЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЈ
СНЕуЃЈ![]() ЪЧзјБъдЕуЃЉЃЌЧѓЫФБпаЮ
ЪЧзјБъдЕуЃЉЃЌЧѓЫФБпаЮ![]() ЕФУцЛ§ЕФзюаЁжЕЃЎ
ЕФУцЛ§ЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГзмЙЋЫОдкAЃЌBСНЕиЗжБ№гаМзЁЂввСНИіЯТЪєЙЋЫОЭЌЪБЩњВњФГжжаТФмдДВњЦЗЃЈетСНИіЙЋЫОУПЬьЖМЙЬЖЈЩњВњ50МўВњЦЗЃЉЃЌЫљЩњВњЕФВњЦЗОљдкБОЕиЯњЪл.ВњЦЗНјШыЪаГЁжЎЧАашвЊЖдВњЦЗНјааадФмМьВтЃЌЕУЗжЕЭгк80ЗжЕФЖЈЮЊДЮЦЗЃЌашвЊЗЕГЇдйМгЙЄЃЛЕУЗжВЛЕЭгк80ЗжЕФЖЈЮЊе§ЦЗЃЌПЩвдНјШыЪаГЁ.МьВтдБЭГМЦСЫМзЁЂввСНИіЯТЪєЙЋЫО100ЬьЕФЩњВњЧщПіМАУПМўВњЦЗгЏРћПїЫ№ЧщПіЃЌЪ§ОнШчЯТБэЫљЪОЃК
Бэ1ЃК
МзЙЋЫО | ЕУЗж |
|
|
|
|
|
МўЪ§ | 10 | 10 | 40 | 40 | 50 | |
ЬьЪ§ | 10 | 10 | 10 | 10 | 80 |
Бэ2ЃК
ввЙЋЫО | ЕУЗж |
|
|
|
| |
МўЪ§ | 10 | 5 | 40 | 45 | 50 | |
ЬьЪ§ | 20 | 10 | 20 | 10 | 70 |
Бэ3ЃК
УПМўе§ЦЗ | УПМўДЮЦЗ | |
МзЙЋЫО | гЏ2ЭђдЊ | Пї3ЭђдЊ |
ввЙЋЫО | гЏ3ЭђдЊ | Пї3.5ЭђдЊ |
ЃЈ1ЃЉЗжБ№ЧѓМзЁЂввСНИіЙЋЫОет100ЬьЩњВњЕФВњЦЗЕФе§ЦЗТЪЃЈгУАйЗжЪ§БэЪОЃЉЃЛ
ЃЈ2ЃЉЪдЮЪМзввСНИіЙЋЫОет100ЬьЩњВњЕФВњЦЗЕФзмРћШѓФФИіИќДѓ?ЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com