
分析 (I)判断f(x)在[0,2]上的单调性,求出f(x)在[0,2]内单调区间端点的函数值,根据零点个数得出k的范围;
(II)令h(x)=f(x)-x,对a进行讨论判断h(x)在[0,+∞)上的单调性,令hmin(x)≤0即可.
解答 解:(I)a=-$\frac{1}{4}$时,f(x)=-$\frac{1}{4}$x2+ln(x+1),
f(x)的定义域为(-1,+∞).
∴f′(x)=-$\frac{1}{2}$x+$\frac{1}{x+1}$,令f′(x)=0得x=1或x=-2(舍).
∴当-1<x<1时,f′(x)>0,当x>1时,f′(x)<0,
∴f(x)在[0,1)上为增函数,在(1,2]上为减函数,
且f(0)=0,f(1)=ln2-$\frac{1}{4}$,f(2)=ln3-1>0.
∵函数g(x)=f(x)-k在[0,2]内有两个零点,
∴方程f(x)=k在[0,2]上有两解,
∴ln3-1≤k<ln2-$\frac{1}{4}$.
(II)令h(x)=f(x)-x=ax2-x+ln(x+1),
则h(x)≤0在[0,+∞)上恒成立,∴hmax(x)≤0.
h′(x)=2ax+$\frac{1}{x+1}$-1,
(1)当a≤0时,2ax≤0,$\frac{1}{x+1}-1$≤0,∴h′(x)=≤0,∴h(x)在[0,+∞)上为减函数,
∴hmax(x)=h(0)=0,符合题意.
(2)当a>0时,令h′(x)=0,即2ax2+(2a-1)x=0,解得x=0或x=$\frac{1-2a}{2a}$=$\frac{1}{2a}$-1.
①若$\frac{1}{2a}-1$≤0,即a≥$\frac{1}{2}$时,h′(x)≥0在[0,+∞)上恒成立,
∴h(x)在[0,+∞]上为增函数,∴当x>0时,h(x)>h(0)=0,不符合题意.
②若$\frac{1}{2a}-1$>0,即0<a$<\frac{1}{2}$时,则当x∈(0,$\frac{1}{2a}-1$)时,h′(x)<0,当x∈($\frac{1}{2a}-1$,+∞)时,h′(x)>0.
∴h(x)在[0,$\frac{1}{2a}-1$)上为减函数,在($\frac{1}{2a}-1$,+∞)上为增函数,
且x→+∞时,h(x)→+∞,不符合题意.
综上,a的取值范围是(-∞,0].
点评 本题考查了函数的单调性与极值,函数零点的判断,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,-8,-4) | B. | (1,8,4) | C. | (-1,-8,-4) | D. | (1,-8,-4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图(1),在三角形PCD中,AB为其中位线,且2BD=PC=2$\sqrt{6}$,CD=2$\sqrt{2}$,若沿AB将三角形PAB折起,使∠PAD=120°,构成四棱锥P-ABCD,如图(2),E和F分别是棱CD和PC的中点,
如图(1),在三角形PCD中,AB为其中位线,且2BD=PC=2$\sqrt{6}$,CD=2$\sqrt{2}$,若沿AB将三角形PAB折起,使∠PAD=120°,构成四棱锥P-ABCD,如图(2),E和F分别是棱CD和PC的中点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
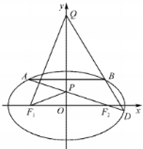 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,且椭圆C上一点M与椭圆左右两个焦点构成的三角形周长为4+2$\sqrt{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,且椭圆C上一点M与椭圆左右两个焦点构成的三角形周长为4+2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com