Question

9．（1）从集合{0，1，2，3}中任取一个数x，从集合{0，1，2}中任取一个数y，求x＞y的概率．
（2）从区间[0，3]中任取一个数x，从区间[0，2]中任取一个数y，求x＞y的概率．

Answer 1

分析 （1）从集合{0，1，2，3}中任取一个数x，从集合{0，1，2}中任取一个数y，根据古典概型的概率公式即可求x＞y的概率．
（2）从区间[0，3]中任取一个数x，从区间[0，2]中任取一个数y，则$\left\{\begin{array}{l}{0≤x≤3}\\{0≤y≤2}\end{array}\right.$，求出对应的面积，利用几何概型的概率公式进行计算．

解答 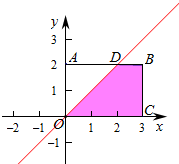解：（1）从集合{0，1，2，3}中任取一个数x，从集合{0，1，2}中任取一个数y，共有4×3=12种，
若x=3，则y=0，1，2，
若x=2，则y=0，1，
若x=1，则y=0，共有6种，
此时x＞y的概率为P=$\frac{6}{12}=\frac{1}{2}$．
（2）从区间[0，3]中任取一个数x，从区间[0，2]中任取一个数y，
则$\left\{\begin{array}{l}{0≤x≤3}\\{0≤y≤2}\end{array}\right.$，对应的区域为矩形，
作出不等式组对应的平面区域如图：
则D（2，2），△OAD的面积S=$\frac{1}{2}×2×2=2$，
则阴影部分的面积S=3×2-2=4，
则从区间[0，3]中任取一个数x，从区间[0，2]中任取一个数y，x＞y的概率的概率P=$\frac{4}{6}=\frac{2}{3}$．

点评 本题主要考查古典概型和几何概型的概率的计算，根据相应的公式是解决本题的关键．