
【题目】函数![]()
(1)当![]() 时,求函数
时,求函数![]() 的定义域;
的定义域;
(2)若![]()
![]() ,请判定
,请判定![]() 的奇偶性;
的奇偶性;
(3)是否存在实数![]() ,使函数
,使函数![]() 在
在![]() 递增,并且最大值为1,若存在,求出
递增,并且最大值为1,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)定义域为![]() ;(2)奇函数;(3)存在,
;(2)奇函数;(3)存在,![]() .
.
【解析】
试题分析:(1)当![]() 时,函数
时,函数![]() 的定义域为
的定义域为![]() ,
,![]() ;(2)
;(2)![]() ,函数
,函数![]() 的定义域为
的定义域为![]() ,即
,即![]() ,关于原点对称,又
,关于原点对称,又![]() ,所以函数
,所以函数![]() 为奇函数;(3)假设存在,设
为奇函数;(3)假设存在,设![]() ,由于
,由于![]() ,所以
,所以![]() 在区间
在区间![]() 上单调递减,若底数
上单调递减,若底数![]() ,根据复合函数单调性可知,函数
,根据复合函数单调性可知,函数![]() 在区间
在区间![]() 上单调递减,不符合题意,若底数
上单调递减,不符合题意,若底数![]() ,根据复合函数单调性可知,函数
,根据复合函数单调性可知,函数![]() 在区间
在区间![]() 上单调递增,所以当
上单调递增,所以当![]() 时,取得最大值1,即
时,取得最大值1,即![]() ,
,![]() ,所以
,所以![]() ,符合题意.
,符合题意.
试题解析:(1)由题意:![]() ,
,![]() ,即
,即![]() ,
,
所以函数![]() 的定义域为
的定义域为![]() .
.
(2)易知![]()
![]() ,
,
∵![]() ,且
,且![]() ,∴
,∴![]() ,关于原点对称,
,关于原点对称,
又∵![]()
![]() =
=![]() ,
,
∴![]()
![]() =-
=-![]() =-
=-![]() ,
,
∴![]() 为奇函数.
为奇函数.
(3)令![]() ,
, ![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
又∵函数![]() 在
在![]() 递增, ∴
递增, ∴![]() ,
,
又![]() 函数
函数![]() 在
在![]() 的最大值为1,
的最大值为1,![]() ,
,
即![]() ,
,![]() .
.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() ,圆
,圆![]() 是以
是以![]() 的中点为圆心,
的中点为圆心, ![]() 为半径的圆.
为半径的圆.
(Ⅰ)若圆![]() 的切线在
的切线在![]() 轴和
轴和![]() 轴上截距相等,求切线方程;
轴上截距相等,求切线方程;
(Ⅱ)若![]() 是圆
是圆![]() 外一点,从
外一点,从![]() 向圆
向圆![]() 引切线
引切线![]() ,
, ![]() 为切点,
为切点, ![]() 为坐标原点,且有
为坐标原点,且有![]() ,求使
,求使![]() 最小的点
最小的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() ,
,![]() 为常数
为常数
(1)用![]() 表示
表示![]() 的最小值,求
的最小值,求![]() 的解析式
的解析式
(2)在(1)中,是否存在最小的整数![]() ,使得
,使得![]() 对于任意
对于任意![]() 均成立,若存在,求出
均成立,若存在,求出![]() 的值;若不存在,请说明理由
的值;若不存在,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
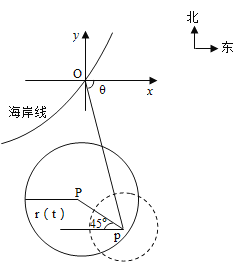
【题目】在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市![]() (如图)的东偏南
(如图)的东偏南![]() 方向300km的海面
方向300km的海面![]() 处,并以20km/h的速度向西偏北
处,并以20km/h的速度向西偏北![]() 方向移动,台风侵袭的范围为圆形区域,当前半径为60km,并以10km/h的速度不断增大,问几小时后该城市开始受到台风的侵袭?受到台风侵袭的时间有多少小时?
方向移动,台风侵袭的范围为圆形区域,当前半径为60km,并以10km/h的速度不断增大,问几小时后该城市开始受到台风的侵袭?受到台风侵袭的时间有多少小时?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A,B,若A不是B的子集,则下列命题中正确的是( )
A.对任意的a∈A,都有aB
B.对任意的b∈B,都有bA
C.存在a0 , 满足a0∈A,a0B
D.存在a0 , 满足a0∈A,a0∈B
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)某旅行社设计了一个组织旅游团包飞机去广州旅游的方案,其中旅行杜的包机费用为![]() 元,旅游团中最多能有
元,旅游团中最多能有![]() 人,并且旅游团中的人数
人,并且旅游团中的人数![]() (单位:个)与每个人交给旅行社的费用
(单位:个)与每个人交给旅行社的费用![]() (单位:元)的关系如下:
(单位:元)的关系如下: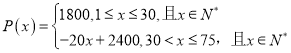 .
.
(1)将旅行社的利润![]() (单位:元)表示成旅游团中的人数
(单位:元)表示成旅游团中的人数![]() 的函数(注:利润=收取的费用一包机费用);
的函数(注:利润=收取的费用一包机费用);
(2)当旅游团有多少人时,旅行社的利润最大?并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com