
【题目】设函数![]() ,
,![]() ,
,![]() 为常数
为常数
(1)用![]() 表示
表示![]() 的最小值,求
的最小值,求![]() 的解析式
的解析式
(2)在(1)中,是否存在最小的整数![]() ,使得
,使得![]() 对于任意
对于任意![]() 均成立,若存在,求出
均成立,若存在,求出![]() 的值;若不存在,请说明理由
的值;若不存在,请说明理由
【答案】(1)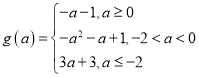 ;(2)存在,
;(2)存在,![]() 的最小值为0.
的最小值为0.
【解析】
试题分析:(1)函数![]() 图象为开口向上的抛物线,对称轴方程为
图象为开口向上的抛物线,对称轴方程为![]() ,下面分情况讨论,当
,下面分情况讨论,当![]() ,即
,即![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递增,所以当
上单调递增,所以当![]() 时,
时,![]() ,当
,当![]() ,即
,即![]() 时,函数
时,函数![]() 在区间
在区间![]() 上先递减,后递增,所以当
上先递减,后递增,所以当![]() 时,函数
时,函数![]() ,当
,当![]() ,即
,即![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递减,所以当
上单调递减,所以当![]() 时,
时,![]() ,所以函数
,所以函数![]() 的最小值
的最小值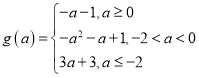 ;(2)是否存在最小的整数
;(2)是否存在最小的整数![]() 使得
使得![]() 对任意的
对任意的![]() 均成立,实际为
均成立,实际为![]() ;经分析可知,函数
;经分析可知,函数![]() 在
在![]() 是增函数,在
是增函数,在![]() 是减函数,所以
是减函数,所以![]() ,则
,则![]() ,所以
,所以![]() 的最小值为0.
的最小值为0.
试题解析:(1)对称轴![]() ,
,
①当![]() 时,
时,![]() 在
在![]() 上是增函数,当
上是增函数,当![]() 时有最小值
时有最小值![]()
②当![]() 时,
时,![]() 在
在![]() 上是减函数,
上是减函数,![]() 时有最小值
时有最小值![]()
③当![]() 时,
时,![]() 在
在![]() 上是不单调,
上是不单调,![]() 时有最小值
时有最小值![]()
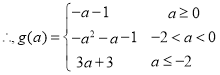
(2)存在, 由题知![]() 在
在![]() 是增函数,在
是增函数,在![]() 是减函数
是减函数
![]() 时,
时,![]() ,
,
![]() 恒成立
恒成立![]() ,
,![]()
![]() 为整数,
为整数,![]() 的最小值为
的最小值为![]()


科目:高中数学 来源: 题型:
【题目】某班级有50名学生,现要采取系统抽样的方法在这50名学生中抽出10名学生,将这50名学生随机编为1~50号,并进行分组,第一组1~5号,第二组6~10号,…,第十组46~50号.若在第三组中抽得号码为12的学生,则在第九组中抽得号码为_____的学生.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线l交抛物线y2=2x于A、B两点,且OA⊥OB,则直线l过定点( )
A. (1,0) B. (2,0) C. (3,0) D. (4,0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]()
(1)当![]() 时,求函数
时,求函数![]() 的定义域;
的定义域;
(2)若![]()
![]() ,请判定
,请判定![]() 的奇偶性;
的奇偶性;
(3)是否存在实数![]() ,使函数
,使函数![]() 在
在![]() 递增,并且最大值为1,若存在,求出
递增,并且最大值为1,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品按行业生产标准分成![]() 个等级,等级系数
个等级,等级系数![]() 依次
依次![]() ,其中
,其中![]() 为标准
为标准![]() ,
,![]() 为标准
为标准![]() .已知甲厂执行标准
.已知甲厂执行标准![]() 生产该产品,产品的零售价为
生产该产品,产品的零售价为![]() 元/件;乙厂执行标准
元/件;乙厂执行标准![]() 生产该产品,产品的零售价为
生产该产品,产品的零售价为![]() 元/件,假定甲、乙两厂的产品都符合相应的执行标准.
元/件,假定甲、乙两厂的产品都符合相应的执行标准.
(1)已知甲厂产品的等级系数![]() 的概率分布如下所示:
的概率分布如下所示:
|
|
|
|
|
|
|
|
|
|
且![]() 的数学期望
的数学期望![]() ,求
,求![]() 的值;
的值;
(2)为分析乙厂产品的等级系数![]() ,从该厂生产的产品中随机抽取
,从该厂生产的产品中随机抽取![]() 件,相应的等级系数组成一个样本,数据如下:
件,相应的等级系数组成一个样本,数据如下:

用这个样本的频率分布估计总体分布,将频率视为概率,求等级系数![]() 的数学期望;
的数学期望;
(3)在(1)、(2)的条件下,若以“性价比”为判断标准,则哪个工厂的产品更具可购买性?说明理由.注:①产品的“性价比”![]() ;
;
②“性价比”大的产品更具可购买性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方
图:
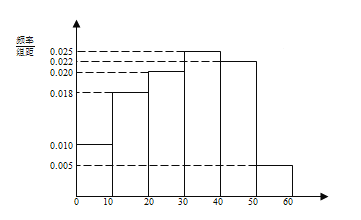
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.
(Ⅰ)根据已知条件完成下面的![]() 列联表,并据此资料,在犯错误的概率不超过
列联表,并据此资料,在犯错误的概率不超过![]() 的前提下,你是否有理由认为“体育迷”与性别有关?
的前提下,你是否有理由认为“体育迷”与性别有关?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
(Ⅱ)将上述调查所得到的频率视为概率,现在从该地区大量电视观众中,采用随机抽样方法每次抽取1名观众,抽取3次,记被抽取的3名观众中的“体育迷”人数为![]() .若每次抽取的结果是相互独立的,求
.若每次抽取的结果是相互独立的,求![]() 的分布列,期望
的分布列,期望![]() 和方差
和方差![]() .
.
附: 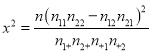
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com