
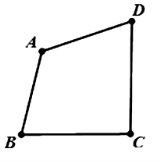
【题目】如图,在凸四边形![]() 中,
中,![]() 为定点,
为定点,![]() ,
,![]() 为动点,满足
为动点,满足![]() .
.
(1)写出![]() 与
与![]() 的关系式;
的关系式;
(2)设△BCD和△ABD的面积分别为![]() 和
和![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1) ![]() (2)
(2) ![]()
【解析】
试题分析:(Ⅰ)在三角形BCD和三角形BCD中,利用余弦定理表示出BD2,两者相等表示即可得到cosC与cosA的关系式;(Ⅱ)利用三角形面积公式变形出S与T,进而表示出![]() ,将第一问表示出的cosA代入得到关于cosC的二次函数,利用二次函数性质即可求出
,将第一问表示出的cosA代入得到关于cosC的二次函数,利用二次函数性质即可求出![]() 的最大值
的最大值
试题解析:(Ⅰ)连接BD,
∵CD=![]() ,AB=BC=DA=1,
,AB=BC=DA=1,
∴在△BCD中,利用余弦定理得:BD2=BC2+CD2-2BCCDcosC=4-2![]() cosC;
cosC;
在△ABD中,BD2=2-2cosA,
∴4-2![]() cosC=2-2cosA,
cosC=2-2cosA,
则cosA=![]() cosC-1
cosC-1
(II)![]()
![]()
![]() …
…
![]()
由题意易知,![]() ,所以
,所以![]()
当![]() 时,
时,![]() 有最大值
有最大值![]() .
.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的图象过点
的图象过点![]() ,对任意
,对任意![]() 满足
满足![]() ,且最小值是
,且最小值是![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)设函数![]() ,其中
,其中![]() ,求
,求![]() 在区间
在区间![]() 上的最小值
上的最小值![]() ;
;
(3)若在区间![]() 上,函数
上,函数![]() 的图象恒在函数
的图象恒在函数![]() 的图象上方,试确定实数
的图象上方,试确定实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() ,
,![]() 为常数
为常数
(1)用![]() 表示
表示![]() 的最小值,求
的最小值,求![]() 的解析式
的解析式
(2)在(1)中,是否存在最小的整数![]() ,使得
,使得![]() 对于任意
对于任意![]() 均成立,若存在,求出
均成立,若存在,求出![]() 的值;若不存在,请说明理由
的值;若不存在,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A,B,若A不是B的子集,则下列命题中正确的是( )
A.对任意的a∈A,都有aB
B.对任意的b∈B,都有bA
C.存在a0 , 满足a0∈A,a0B
D.存在a0 , 满足a0∈A,a0∈B
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出;当每辆车的月租金每增加50元时,未租出的车将会增加一辆,租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金为多少元时,租赁公司的月收益最大?最大收益为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)某旅行社设计了一个组织旅游团包飞机去广州旅游的方案,其中旅行杜的包机费用为![]() 元,旅游团中最多能有
元,旅游团中最多能有![]() 人,并且旅游团中的人数
人,并且旅游团中的人数![]() (单位:个)与每个人交给旅行社的费用
(单位:个)与每个人交给旅行社的费用![]() (单位:元)的关系如下:
(单位:元)的关系如下: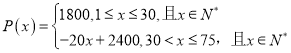 .
.
(1)将旅行社的利润![]() (单位:元)表示成旅游团中的人数
(单位:元)表示成旅游团中的人数![]() 的函数(注:利润=收取的费用一包机费用);
的函数(注:利润=收取的费用一包机费用);
(2)当旅游团有多少人时,旅行社的利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用系统抽样法从160名学生中抽取容量为20的样本,将160名学生从1~160编号,按编号顺序平均分成20组(1~8号,9~16号,。。。,153~160号).若第15组应抽出的号码为116,则第一组中用抽签方法确定的号码是( )
A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com