
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
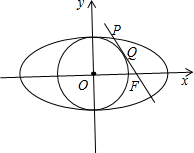
| |0-kc| | ||
|
| b | ||
|
|
|
|
| 2b2-c2 |
| c |
2b
| ||
| c |
| (2b2-c2)2 |
| a2c2 |
| 4b2(c2-b2) |
| b2c2 |
| c |
| a |
| ||
| 3 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| m |
| n |
| m |
| n |
| A、8 | B、16 | C、4 | D、2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| IG |
| F1F2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
A、[
| ||||||||
B、[
| ||||||||
C、[
| ||||||||
D、[
|
查看答案和解析>>
科目:高中数学 来源:2015届山东省高三上学期11月检测考试理科数学试卷(解析版) 题型:解答题
(本小题满分12分)在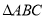 中,内角
中,内角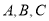 所对的边分别为
所对的边分别为 。已知
。已知
(1)求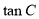 的值;
的值;
(2)若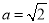 ,求
,求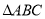 的面积
的面积
查看答案和解析>>
科目:高中数学 来源:2015届山东省德州市高三10月月考理科数学试卷(解析版) 题型:解答题
统计表明,某种型号的汽车在匀速行驶中每小时的耗油量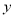 (升)关于行驶速度
(升)关于行驶速度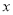 (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为: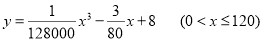 ,已知甲、乙两地相距100千米
,已知甲、乙两地相距100千米
(1)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com