已知椭圆C
1:
+=1(a>b>0)与圆C
2:x
2+y
2=b
2,若在椭圆C
1上存在点P,使得由点P所作的圆C
2的两条切线互相垂直,则椭圆C
1的离心率的取值范围是( )
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设P(m,n),则由题意知
,由此导出e=
=
,从而能求出椭圆C
1的离心率的取值范围.
解答:解:设P(m,n),则由题意知:
,
∴b
2m
2=
a2-a2 n2=
a2•,
∴
=
,
∴e=
=
=
=
,
∵-a≤m≤a,
∴m=b时,e
max→
=1,
m=a时,e
min=
=
,∴
=
,
∴e
min=
=
.
故选:C.
点评:本题考查椭圆的离心率的取值范围的求法,是中档题,解题时要认真审题,注意椭圆性质的灵活运用.
练习册系列答案
相关习题
科目:高中数学
来源:
题型:
已知集合A={x|-3<x<3},B={x|x>1},则集合A∩B为( )
| A、[0,3) |
| B、[1,3) |
| C、(1,3) |
| D、(-3,1] |
查看答案和解析>>
科目:高中数学
来源:
题型:
集合A={x|2x≥1},则∁RA=( )
| A、(-∞,0] |
| B、(-∞,0) |
| C、[0,+∞) |
| D、(0,+∞) |
查看答案和解析>>
科目:高中数学
来源:
题型:
过椭圆
+
=1(a>b>0)的右焦点F(c,0)作圆x
2+y
2=b
2的切线FQ(Q为切点)交椭圆于点P,当点Q恰为FP的中点时,椭圆的离心率为( )
查看答案和解析>>
科目:高中数学
来源:
题型:
已知两定点A(-2,0)和B(2,0),动点P(x,y)在直线l:y=x+3上移动,椭圆C以A,B为焦点且经过点P,则椭圆C的离心率的最大值为( )
查看答案和解析>>
科目:高中数学
来源:2015届山东省高三第一次诊断性考试文科数学试卷(解析版)
题型:选择题
查看答案和解析>>
科目:高中数学
来源:2015届山东省高三第一次诊断性考试文科数学试卷(解析版)
题型:选择题
已知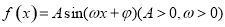 在
在 处取最大值,则
处取最大值,则
A.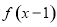 一定是奇函数
一定是奇函数
B.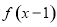 一定是偶函数
一定是偶函数
C.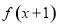 一定是奇函数
一定是奇函数
D.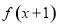 一定是偶函数
一定是偶函数
查看答案和解析>>
科目:高中数学
来源:2015届山东省高三上学期11月检测考试理科数学试卷(解析版)
题型:选择题
已知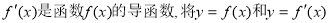 的图象画在同一个直角坐标系中,不可能正确的是( )
的图象画在同一个直角坐标系中,不可能正确的是( )

查看答案和解析>>
科目:高中数学
来源:2015届山东省德州市高三10月月考理科数学试卷(解析版)
题型:选择题
曲线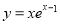 在点(1,1)处切线的斜率等于( )
在点(1,1)处切线的斜率等于( )
A.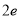 B.
B.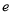 C.2 D.1
C.2 D.1
查看答案和解析>>



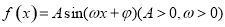 在
在 处取最大值,则
处取最大值,则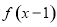 一定是奇函数
一定是奇函数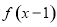 一定是偶函数
一定是偶函数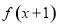 一定是奇函数
一定是奇函数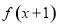 一定是偶函数
一定是偶函数